Deseja-se construir uma peça de zinco que tem a forma da superfície de equação , compreendida entre os planos e e o cilindro . Se o metro quadrado do zinco custa reais, calcule o preço total da peça.
Passo 1
Vamos entender essa questão antes de qualquer coisa, ele nos diz um valor de preço por metro quadrado, certo? Se ele quer saber o preço total da peça, precisamos saber quantos metros quadrados tem a superfície, em outras palavras, precisamos calcular a sua área!
Para o cálculo da área de uma superfície, vamos usar essa integral aqui
Portanto precisamos parametrizar a superfície do enunciado, determinar seus limites e calcular sua normal. Depois é só colocar tudo isso na integral e resolver, vamos lá?
Passo 2
Vamos visualizar melhor a nossa superfície, o enunciado diz que tem a forma da equação
Portanto podemos parametrizar de forma explícita assim:
O esboço descrito pelo enunciado é esse aqui:
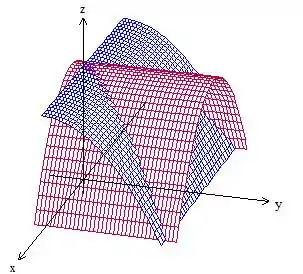
Perceba que a superfície de interesse é a vermelha, pois é a de equação , se quiséssemos visualizar somente ela seria assim
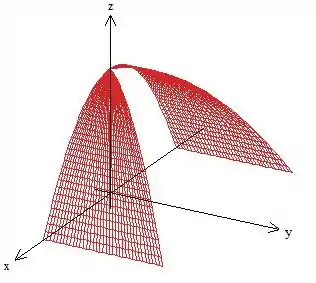
Dentro da nossa parametrização explícita, vamos projetar essa superfície no plano :
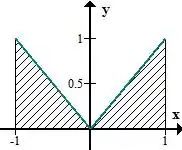
Podemos chegar nessa função igualando e
Vamos ter que dividir esse limite em dois, o primeiro quando é negativo
O segundo quando é positivo
Passo 3
Definida a parametrização e os limites, vamos agora para o vetor normal, como a nossa parametrização é explícita, podemos usar aquele macete:
Para uma função , a normal vai ser dada por
As derivadas de vão ser
Logo a nossa normal é dada por:
Passo 4
Para a integral não precisamos somente da normal , precisamos do seu módulo, vamos fazer isso agora:
Passo 5
Botando tudo na integral:
Vamos fazer uma substituição aqui:
Voltando para a integral e trocando tudo isso:
Podemos juntar essas duas integrais né? Só invertermos a segunda
Passo 6
Esse é o valor da área, certo? A única diferença no enunciado é que ele nos pede o preço teórico da superfície. Não tem problema, se essa é a área e o valor do metro quadrado é , o valor total da peça vai ser