Encontre a área da superfície que está acima do triângulo com vértices , e .
Passo 1
Vamos, antes de tudo, desenhar essa superfície para termos uma ideia melhor do problema. Temos a equação . Sabe o que é isso? Bom, eu também não sabia! Vivendo e aprendendo né.
Você não precisa disso para resolver a questão, mas se estiver curioso, é essa superfície aí (meio que um cilindro de parábola distorcido):

O problema pede a área dessa superfície que está limitada pelo triângulo abaixo:
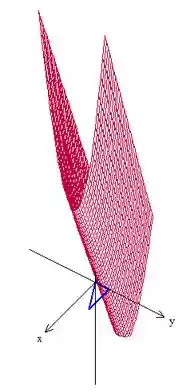
É como se esse triângulo se estendesse ao longo do eixo e cortasse a superfíce vermelha, sacou?
Beleza, vamos usar essa fórmula aqui para calcular a área da superfície:
Passo 2
Agora precisamos parametrizar a superfície. Como nossa equação é , vamos usar e como parâmetros, ok? Temos então:
Onde e se encontram dentro do triângulo que desenhamos no passo anterior, a projeção da nossa superfíce cortada no plano .
Passo 3
Calcular e
Passo 4
Calcular
Passo 5
Agora vamos montar a integral
Onde é a região dentro no triângulo. Vamos ver esse triângulo de cima, para poder descrever a região:
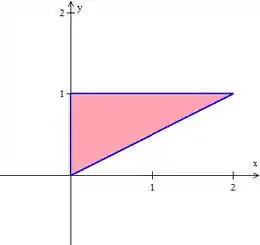
Já podemos dizer que , pela figura. Agora vamos encontrar o intervalo de . Escrevendo a região como do tipo II, tem que estar limitado por funções.
Pelo gráfico, vemos que varia desde até a reta inclinada (que liga os pontos e ). Vamos então achar a equação dessa reta inclinada.
Temos a equação geral da reta . Substituindo os pontos da reta:
A equação da reta é então , ou . Assim, podemos escrever .
Levando os intervalos que encontramos para a integral:
Passo 6
Agora vamos resolver essa integral aí. Integrando em relação a , temos:
Agora vamos fazer a substituição
Levando isso para a integral, temos:
Agora é só integrar