Questão 4: Considere o corpo sólido no interior do cilindro , limitado por cima e por baixo pelo cone . Calcule a área de superfície de .
Sugestão: Evite a parametrização do cilindro como superfície de revolução com eixo deslocado!
Passo 1
Pois bem, se o problema nos pediu área de superfície isso só pode significar uma coisa: que ele nos quer avaliar se sabemos calcular uma integral de superfície escalar:
Essa é basicamente a nossa tarefa, é encontrar a superfície que delimita (a gente nomeia assim ) e calcular integrais! =)
Então bora?
Passo 2
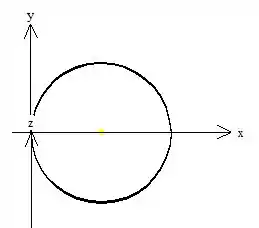
Se vamos encontrar a área de um sólido, antes é legal a gente desenhar esse sólido, não é mesmo?
Como o próprio problema nos pediu, esse sólido é composto por um cilindro deslocado da origem em uma unidade :
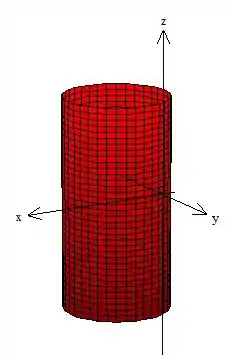
E também ele é delimitado por um cone com vértice na origem:
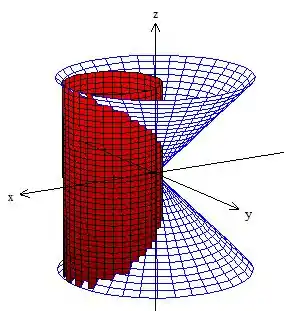
E basicamente o nosso sólido é esse camarada aí dentro dessas duas superfícies !
Acho que dá para notar que embora esse sólido tenha três superfícies delimitadoras, só precisamos calcular de duas: a da casca cilíndrica e do teto cônico, porque a área da base cônica será a mesma do teto, saca? Então se consideramos a parte cilíndrica como superfície e a parte do teto de cone como , a área total de será dada por...
Passo 3
Vamos então começar pela integral de superfície do cilindro:
Vamos precisar de:
- Parametrizar a superfície .
- Encontrar o termo .
Para parametrizar, bem, como é um cilindro vamos parametrizar com a forma clássica (seguindo as coordenadas polares):
Agora, como você já sabe, uma parametrização de superfície tem que depender apenas de duas variáveis (que são os dois parâmetros). No caso do cilindro vamos ter que trocar o . Mas agora, por qual valor vamos trocar? Vamos ver a equação novamente:
Veja que esse cilindro tem raio e está deslocado em , então, se a gente fosse utilizar parametrização com eixo deslocado, faríamos:
Porém!!! O problema nos sugeriu que evitássemos essa parametrização, e eu não sei você, mas se o problema nos sugeriu, acho melhor obedecer, neh? (Mas quero deixar claro que essa parametrização não está errada).
Ok! Então qual vamos utilizar? Bem, se substituirmos as coordenadas polares na equação do cilindro, talvez possamos ter uma resposta...
OPA!!! Então encontramos o valor de no eixo original de coordenadas ! Assim, a nossa parametrização fica:
Ou de uma forma mais elegante:
Passo 4
A má notícia nesse passo é que ainda não acabou a parametrização do passo anterior, afinal de contas, o problema só acaba quando temos também os limites dos parâmetros em mãos, e é isso que vãos fazer aqui agora!
Primeiro vamos falar de , onde ele varia?
É importante notar das diferenças de parametrização. Se tivéssemos trabalhando com o eixo deslocado (coloquei de amarelo)...
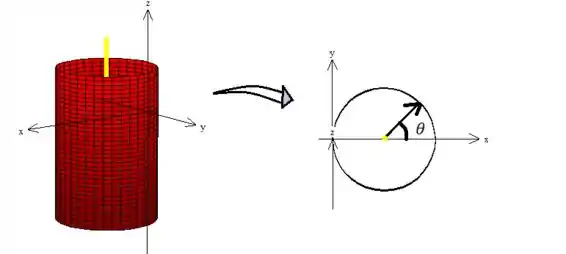
O estaria variando de a (ou dando uma volta completa também serve).
PORÉM... Estamos trabalhando uma parametrização que não deslocou o eixo, ou seja, continuamos aqui:
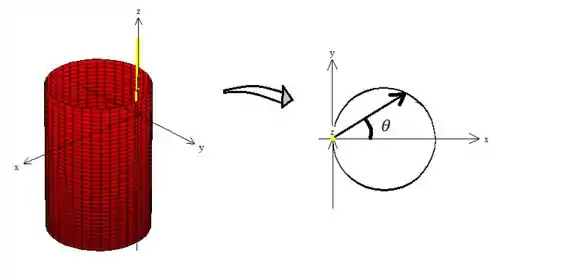
Assim... O no NOSSO CASO, está variando de baixo pra cima, ou seja:
Já o , bem... O cilindro está delimitado em cima e embaixo pelo cone, então basta substituir a parametrização na equação do cone:
Então...
Passo 5
Com a parametrização concluída, podemos encontrar então o termo ...
Sendo o vetor norma determinado através da parametrização:
Como
Derivando...
E aplicando o produto vetorial...
Ou...
Extraindo o módulo...
Então...
Passo 6
Então agora podemos regressar a integral de superfície e substituir mesmo...
Passo 7
ACHOU QUE ACABOU? Bem, infelizmente ainda não campeão ! Ainda falta a outra integral (a integral que calcula área da parte cônica):
Como fizemos anteriormente, precisamos:
- Parametrizar .
- Encontra .
Bem, agora vamos parametrizar um cone:
Logo, uma boa parametrização para a parte de cima do cone é:
Onde os parâmetros e estão variando? Bem, essa é mais fácil, pois só queremos o pedaço que está dentro do cilindro, ou seja:
Resumindo, o e o , variam no disco de raio que está deslocado da origem !
Passo 8
Para encontrar o dessa superfície aí, vai ser mais fácil, pois como realizamos uma parametrização como uma função de e , podemos utilizar o bizu para o vetor normal:
Portando o módulo será:
Portanto...
Passo 9
Novamente retornando para o cálculo da integral de superfície:
Epa!!! Essa integral dupla aí representa a área, no caso é a área da região de variação do e . Como a região de variação do e é um disco de raio ...
Então:
Passo 10
Calma, garoto! Eu sei que você está louco para terminar o problema, mas ainda temos que retornar para o que queremos desde o princípio: a área da região de :
Resposta
Exercícios de Livros Relacionados
Ver Mais
Ver Mais
Ver Mais
Ver Mais
Ver Mais