Questão :
a) Seja a parte do cilindro que está no interior do cilindro com . Calcule a massa de sendo a densidade .
Passo 1
A essa altura do campeonato, massa de superfície não é nada mais nada menos que uma integral de superfície escalar. Mas não é qualquer integral de superfície e sim esta daqui oh:
A boa notícia é que uma integral dessa forma tem um passo a passo bem legal que nos ajuda muito:
1º - Parametrizar a superfície .
2º - Substituir os termos da parametrização na função densidade .
3º - Encontrar o termo .
Bora lá?
Passo 2
Devemos parametrizar a superfície , mas por falar nisso quem é ela? Seria muito bom se tivéssemos uma visão mais geométrica dela, então desenhemos esses dois cilindros juntos e vamos ver no que dá:
é a parte desse cilindro deitado ao redor de , ...
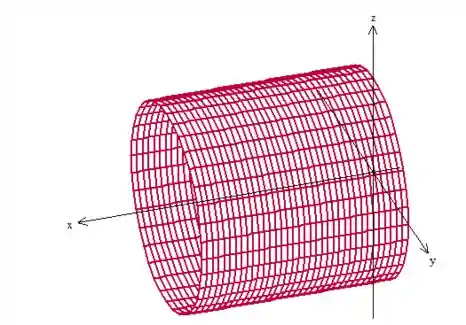
Mas está delimitado pelo cilindro em pé ao redor de e também pelo chão ...
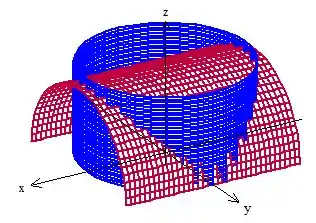
Eis a superfície !
Passo 3
Temos que parametrizar esse cara. Bem, podemos fazer isso de uma forma explícita caso explicitarmos o em sua equação...
Como se trata da parte de cima...
Veja que o e o são os próprios parâmetros dessa superfície. O já é uma função deles, saca? Então a parametrização legal que fizemos foi:
Passo 4
Nunca concluímos uma parametrização sem antes dizer onde os parâmetros, o que no caso são o e o , estão variando.
Essa etapa pra nós não é muito chata, pois pensa comigo: A superfície é o cilindro deitado certo? Então qual é o papel desse cilindro em pé?
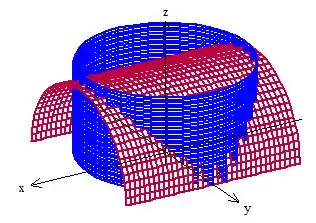
Exatamente, delimitar a parte da superfície que queremos, ou seja, a parte que queremos de superfície é de tal que ela está dentro do cilindro em pé. Então o e o da superfície, variam nesse círculo de raio aí:
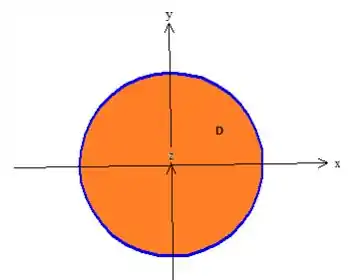
Por hora, apenas vamos dizer que:
Depois se precisar descrevemos como polar e tal ;)
Passo 5
Pelo passo a passo legal do passo , é hora de substituir os parâmetros da parametrização:
Na função que estamos integrando:
Ou seja...
Passo 6
Para encontrar o termo ...
Onde o vetor normal, usualmente pode ser determinado por, calculando:
Calculando essas derivadas parciais...
Calculando a outra derivada parcial tomando cuidado com a regra da cadeia
Voltando para o produto vetorial lembrando que esse é dado pelo cálculo de um determinante:
Então
Extraindo o módulo...
Então concluímos que o termo que o termo é...
Passo 7
Voltando para a integral e substituindo tudo...
Observe que trocamos o por , afinal agora vamos calcular uma integral dupla em e necessitando do domínio deles, sacou?
Agora é só calcular a integral dupla e correr para o abraço!
Passo 8
Por falar em integral dupla, note que estamos calculando uma integral dentro de uma região circular, sugerindo coordenadas polares:
Para determinar os limites, basta olhar novamente para a região , repare que:
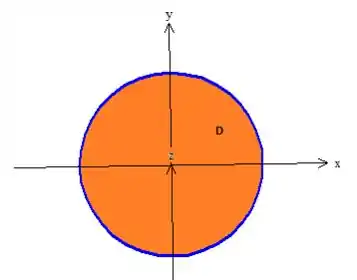
Passo 9
Substituindo na integral dupla que queremos não esquecendo-se do Jacobiano...
Integrando em ...
Substituindo os limite em ...
Lembrando que ...
Integrando...