Um disco de massa e raio desliza ao longo de uma superfície sem atrito com velocidade . Em um dado instante de tempo , ele colide com um outro disco de massa e raio , inicialmente em repouso. A colisão acontece de tal maneira que apenas as bordas dos discos se tocam. Como as bordas dos discos estavam revestidas com uma cola de ação instantânea, os discos ficam grudados e passam a girar após a colisão. Nesse caso, determine os seguintes valores:
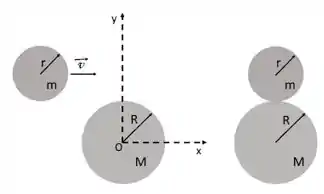
(a) A velocidade do centro de massa do sistema.
(b) A magnitude, direção e sentido do momento angular intrínseco dos discos, após a colisão, em relação ao seu centro de massa.
(c) O valor absoluto da velocidade angular dos discos após a colisão, em relação ao seu centro de massa.
Passo 1
Na letra (a), queremos a velocidade do centro de massa.
Repare que como o sistema está isolado de forças externas, essa velocidade vai ser a mesma a todo instante, seja antes ou depois da colisão.
Antes da colisão, apenas o disco de massa se move, então a velocidade do centro de massa será:
Substituindo os valores, temos:
Passo 2
Na letra (b), queremos o momento angular , após a colisão.
Calcular esse momento angular após a colisão é um pouco mais chato, pois temos tanto um movimento de translação quanto um movimento de rotação para analisarmos.
Porém, uma sacada boa é que o momento angular se conserva, pois temos um sistema isolado.
Então, podemos muito bem calcularmos esse momento em qualquer instante, inclusive antes da colisão, quando temos apenas um corpo em transalação.
Passo 3
Vamos pegar o instante exato antes da colisão:
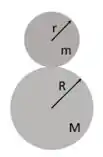
Queremos o momento angular com relação ao centro de massa do sistema, então, vamos calcular a posição desse centro de massa.
Nesse instante exato da colisão, a coordenada será:
Já a coordenada pode ser calculada com:
A coordenada do disco maior está na origem, logo ela é zero. Já a coordenada do disco menor será a soma dos raios:
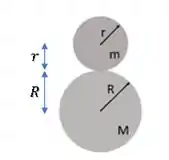
Substituindo os valores, temos:
Passo 4
Agora vamos ao cálculo do momento angular.
Como não há rotação, podemos calcular o momento angular do sistema com a expressão de momento angular de uma partícula considerando o disco que se move em seu centro de massa (centro do disco).
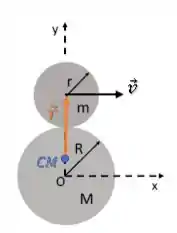
Como os vetores são perpendiculares, o produto vetorial fica apenas o produto dos dois módulos. Porém, o sentido é será:
Lembrando que com a regra da mão direita, temos, inicialmente, nossos dedos apontados para positivo e a mão fechando para a direita no sentido horário, ou seja, palma da mão em positivo , assim, nosso dedão aponta para baixo .
Já sabemos os valores de e de , mas quem será ?
O valor de será a distância até o centro do disco de massa menos a posição do centro de massa:
Substituindo os valores, temos:
Passo 5
Na letra (c), queremos o valor da velocidade angular em torno do CM (centro de massa), após a colisão.
Já temos o momento angular em torno do CM, após a colisão, então podemos descobrir a velocidade angular em torno desse mesmo ponto:
Mas a questão é encontrar esse novo momento de inércia .
Ele será a soma dos momento de inércia de cada disco em torno do CM do sistema:
Passo 6
No formulário, temos que o momento de inércia de um disco em torno de seu centro é:
Porém, queremos o momento de inércia em torno de outro ponto sem ser o centro de cada disco, portanto, temos que usar o teorema dos eixos paralelos:
Então vamos lá, para o disco de massa , o momento de inércia será seu passando pelo centro de massa, enquanto a distância será aquela mesma distância que calculamos no Passo 4:
Já o momento de inércia do disco 2 com relação ao seu centro de massa será:
Assim, temos que o momento de inércia do sistema será:
Passo 7
Agora, basta nós substituirmos na expressão de momento angular que achamos a velocidade angular:
Resposta
(a)
(b)
(c)