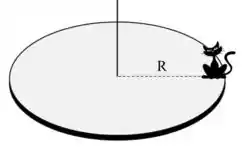
Questão 2) A figura ao lado representa um gato de massa , situado na borda de um disco de raio e massa que gira em torno de um eixo vertical que passa pelo seu centro (como um carrossel) com velocidade angular no sentido anti-horário. De repente o gato salta para fora do disco em uma direção tangente à sua borda.
b). Determine o módulo da velocidade tangencial do gato ao saltar, para que o disco inverta o sentido de rotação, passando a girar no sentido horário com metade da velocidade angular inicial (). O salto deve ocorrer no sentido horário ou anti-horário?
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Temos um disco de massa e raio que gira a uma velocidade angular (anti-horário). Na borda desse disco há um gatinho de massa que inicialmente está parado em relação ao disco.
Então subitamente o gatinho pula do disco com um trajeto tangencial à borda do disco.
Após esse momento, o disco passa a girar a uma velocidade .
Sabendo que , qual deve ser a velocidade tangencial do gato para que a relação seja satisfeita e o gatinho deve pular no sentido horário ou anti-horário?
Tem ideia do que fazer? 🤔🤔
Pelo princípio da conservação do momento angular que discutimos no item a, podemos dizer que , sendo que o salto do gatinho cria uma perturbação no giro do disco, fazendo o mesmo perder ou ganhar velocidade angular.
Entendeu? 😁
Passo 2
Primeiro de tudo, vamos responder se o gatinho deve pular na direção horária ou anti-horária. O que você acha?

Podemos responder essa pergunta a partir da informação de que a velocidade angular final é igual a metade da velocidade angular inicial, ou seja, .
Se quando o gato pula, a velocidade angular diminui, certamente ele exerce uma força contrária ao giro. Ou seja, o disco gira no sentido anti-horário e o gato faz uma força no sentido horário.
Se o gato faz uma força no sentido horário, o salto deve ser no sentido anti-horário já que o atrito entre o gato e o disco acontece no sentido contrário ao movimento. Entendeu?
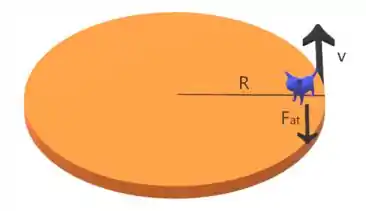
Ou seja, o salto deve ocorrer no sentido anti-horário!
Tranquilo até aqui? 😉
Passo 3
Agora vamos obter a velocidade linear do gato sabendo que e que .
O momento linear pode ser calculado como ou também como , onde é o momento linear do gato (como e são perpendiculares, ).
Vamos lá! Inicialmente vamos calcular como
Então temos que encontrar o momento de inércia do sistema nesse instante.
O gatinho gira a uma distância do eixo de rotação. Considerando ele como um ponto adimensional, temos
Agora para o disco vemos que o seu momento de inércia é o mesmo que o momento de inércia do cilindro, ou seja
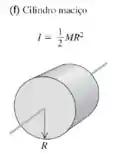
Logo, o momento do sistema é igual a soma de com
Se , então
Substituindo que calculamos em , temos
Entendeu essa parte? 👍
Passo 4
Agora, como o momento angular se conserva por não haver torques externos no sistema, vamos calcular o momento angular final.
Para o disco, vamos fazer a mesma análise que fizemos anteriormente, porém com alguns valores diferentes
Como vimos que , temos
Se e se , vamos obter
Mas e aí, tudo certo? 🤔
No enunciado foi dito que após o pulo do gato, o disco girou no sentido oposto (horário).
Como consideramos o sentido anti-horário como positivo antes, agora temos que considerar esse resultado como negativo.
Interessante, não é? 😎
Passo 5
E o gatinhoo?? 😍
Vamos calcular seu momento angular agora!
A maneira mais conveniente de fazer esse cálculo é usar a equação
Mas como e são perpendiculares pelo fato da trajetória do gatinho ser tangente ao disco, temos que resultando em
Lembra o que é ?
Esse é o momento linear! Que pode ser calculado como o produto da massa pela velocidade de um objeto, ou seja
Substituindo em
Dessa forma, o momento angular total é dado por
Ou seja
Entendeu? 😁
Passo 6
Por fim, aplicando o princípio de conservação do momento angular, temos
Se e se , vamos obter
Passando o para o outro lado com o sinal trocado
Dessa forma, podemos simplificar a equação cortando e dos dois lados
Com isso, vimos que a velocidade que o gatinho deve atingir ao pular do disco para que as condições do enunciado aconteçam é dada por !
Fim! Iae, o que achou? Responde Aí! 😁
