A figura mostra uma barra homogênea vertical de comprimento e massa , em repouso, apoiada em um plano horizontal sem atrito, que pode girar em torno de um eixo em sua extremidade. Veja a figura. Uma partícula de massa e velocidade perpendicular à barra se desloca sobre o plano. Ela colide com a barra em um ponto distante do eixo, ficando grudada na barra.
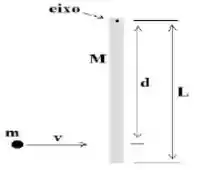
Dado: Haste:
(a) Considere a colisão. Marque com as grandezas físicas conservadas e com as não conservadas. Justifique TODAS as suas escolhas.
1-( ) Momento linear da partícula, pois...
2-( ) Momento linear do sistema barra-partícula, pois...
3-( ) Energia cinética do sistema barra-partícula, pois...
4-( ) Momento angular do sistema barra-partícula em relação ao eixo, pois...
(b) Obtenha uma expressão literal para o valor da velocidade angular do sistema barra-partícula imediatamente após o impacto em função dos dados fornecidos. Justifique claramente a lei física utilizada.
Passo 1
Temos uma partícula que colide com uma barra vertical presa por um eixo.
Queremos analisar quais grandezas que se conservam (se mantêm iguais) e quais que não se conservam (mudam).
Vamos analisar uma por uma...
Passo 2
1-( ) Momento linear da partícula, pois...
O momento linear da partícula é dado por:
Quando ele colide, sua velocidade vai mudar, certo?
Então seu momento linear também vai mudar.
Logo o momento linear da partícula não se conserva (NC).
Isso acontece pois quando consideramos o sistema como apenas a partícula, a força que a barra exerce sobre ela na colisão é uma força externa.
Assim, essa força gera impulso na partícula e altera seu momento linear:
Passo 3
2-( ) Momento linear do sistema barra-partícula, pois...
Agora estamos considerando o sistema como a barra mais a partícula.
O sistema parece isolado, o momento linear vai se conservar?
Esse é o vetor momento linear inicial do sistema:
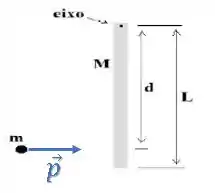
Esse é o vetor momento linear após a colisão, aplicado no centro de massa do sistema:

Eles vão apresentam direções e módulos diferentes.
Então, o momento linear do sistema barra-partícula não se conserva (NC).
Mas o sistema não era isolado?
Na verdade não, pois a barra está presa por um pino na extremidade.
Esse pino vai aplicar exercer uma força externa sobre o sistema barra-partícula, que será uma força externa.
Também temos a força peso como força externa, porém ela é perpendicular ao deslocamento no momento da colisão e não exerce trabalho.
Logo, há impulso sobre o sistema e, portanto, variação do momento linear:
Passo 4
3-( ) Energia cinética do sistema barra-partícula, pois...
Agora, temos que pensar nos tipos de colisões.
Em qual desses tipos os objetos saem juntos da colisão?
Na colisão perfeitamente inelástica, né?
Isso significa que as energias cinéticas são diferentes antes e depois da colisão:
Então, a energia cinética do sistema barra-partícula não se conserva (NC).
Passo 5
4-( ) Momento angular do sistema barra-partícula em relação ao eixo, pois...
Para você que estava ansioso para alguma grandeza se conservar, chegou a hora...
Para saber se o momento angular do sistema se conserva, precisamos olhar para os torques externos:
As forças entre a bolinha e a barra são forças internas e se cancelam.
Só sobra a força que o eixo exerce sobre a barra.
Como a força está aplicada sobre o eixo de rotação, seu torque é nulo.
Além disso, o torque da força peso também será nulo no momento da colisão, uma vez que ele está direção que passa sobre o eixo de rotação.
Então:
Assim, o momento angular se conserva:
Então, a resposta é o momento angular do sistema barra-partícula em relação ao eixo se conserva (C).
Passo 6
Na letra (b), queremos a velocidade angular após a colisão.
Já vimos que o momento angular do sistema se conserva:
O momento angular antes da colisão , será apenas o momento angular da partícula, dado pela multiplicação da distância ao eixo de rotação pelo momento linear da partícula :
Enquanto o momento angular após a colisão , será o momento angular do sistema barra-partícula em rotação:
Conservando o momento angular, temos:
Então, basta descobrir o momento de inércia do sistema barra-partícula que encontramos uma expressão para .
Passo 7
O momento de inércia desse sistema será a soma do momento de inércia da partícula com a da barra:
O momento de inércia da partícula é calculado com:
Como a distância ao eixo de rotação é , temos:
Já para calcular o momento de inércia da barra, temos que utilizar a fórmula do para um eixo passando pelo centro da barra e depois aplicar o teorema dos eixos paralelos para um eixo passando pela extremidade:

Seu momento de inércia com relação ao eixo da extremidade seria:
Onde a distância entre os eixos é metade do comprimento da barra:
Então o momento de inércia do sistema é:
Passo 8
Voltando à nossa expressão para , temos:
Resposta
(a)
1-(NC) Momento linear da partícula, pois existe a força da barra sobre a partícula, assim, temos uma força resultante sobre o sistema (partícula).
2-(NC) Momento linear do sistema barra-partícula, pois existe a força do eixo sobre a barra, assim, temos uma força resultante sobre o sistema barra-partícula.
3-(NC) Energia cinética do sistema barra-partícula, pois a colisão é perfeitamente inelástica.
4-(C) Momento angular do sistema barra-partícula em relação ao eixo, pois o torque resultante externo é zero sobre o sistema barra-partícula durante a colisão, então, não há variação do momento angular.
(b)