PUC-RIO – Física 3 2020.1 – P2– Questão 10
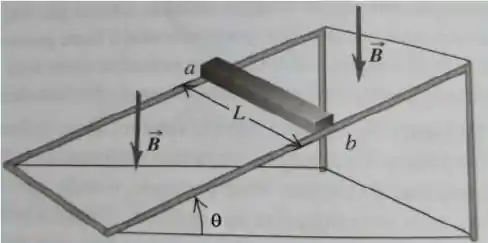
Uma barra de comprimento e resistência desliza, sem atrito, sobre um trilho inclinado por um ângulo de . O conjunto está em um campo magnético , com linhas de campo verticais direcionadas para baixo. A barra é solta a partir do repouso de uma certa altura no trilho e começa a deslizar devido ao seu peso . Qual é o valor da velocidade terminal?
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
A força peso faz deslizar a barra para baixo, certo? Mas ao mesmo tempo a força magnética na barra é para cima, o que compensa a força peso em algum momento e daí temos uma velocidade terminal, que é quando não há força resultante no sistema e ele segue em velocidade constante.
A força magnética é:
Como o campo é vertical, o ângulo entre o fio e o campo é , e o módulo da força é:
Passo 2
Mas a força eletromotriz pode ser dada em termos da variação de fluxo magnético:
Então a força pode ser dada em termos da velocidade terminal:
Passo 3
E agora temos que na direção do movimento (em cima dos trilhos) a força resultante deve ser zero:
Agora é só substituir os valores:
Beleza?
Pronto pra próxima questão? =)