Exercícios de Força Magnética sobre um Fio Condutor - Lista de Exercícios Resolvida
Questão 1
A figura abaixo mostra um fio que conduz uma corrente . Ele é formado por dois trechos retilíneos de comprimento , ambos tangentes à mesma circunferência de raio , e por um arco desta circunferência que subentende um ângulo central de , conforme a figura abaixo.
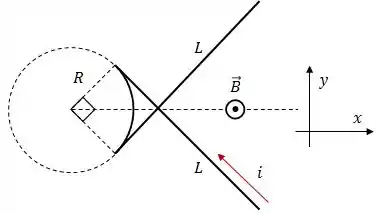
O fio está numa região onde existe um campo magnético uniforme, perpendicular ao plano da página e orientado para fora dela.
Calcule o vetor força magnética que age sobre cada segmento de fio retilíneo;
Calcule o vetor força magnética que age sobre a parte circular;
Calcule a força resultante que age sobre o fio;
Ver solução completaQuestão 2
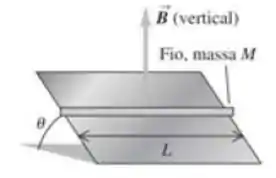
Um fio retilíneo condutor de massa e comprimento é colocado sobre um plano inclinado sem atrito, formando um ângulo com a horizontal, como mostra a Figura abaixo. Existe um campo magnético uniforme ao longo de todos os pontos (produzido por um conjunto de eletroímãs não indicados na Figura). Para impedir que o fio escorregue para baixo do plano, uma fonte de tensão é aplicada nas extremidades do fio. Quando uma corrente com um valor preciso circula no fio, ele permanece em repouso. Determine o módulo e o sentido da corrente que circula para fazer o fio ficar em repouso.
Questão 3
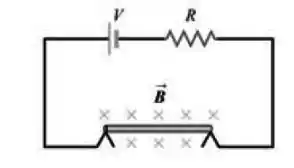
Uma barra metálica delgada, com de comprimento e massa , repousa sobre dois suportes metálicos (mas não está conectada a eles), em um campo magnético uniforme de , como indica a Figura abaixo. Uma bateria com ddp e um resistor de em série estão conectados aos suportes.
- Qual voltagem máxima a bateria pode ter sem romper o circuito nos suportes?
- A voltagem da bateria possui o valor máximo calculado no item (a). Supondo que o resistor repentinamente sofre um curto-circuito parcial, diminuindo sua resistência para , ache a aceleração inicial da barra.
Questão 4
Uma barra de cobre de repousa em dois trilhos horizontais situados a de distância um do outro e é percorrida por uma corrente de . O coeficiente de atrito estático entre os trilhos é . Determine o módulo e o ângulo (em relação à vertical) do menor campo magnético que faz a barra se mover.
Ver solução completaQuestão 5
Um fio fino, transportando uma corrente , é dobrado na forma de um grampo composto por dois segmentos retilíneos de comprimento e um arco semicircular de raio .
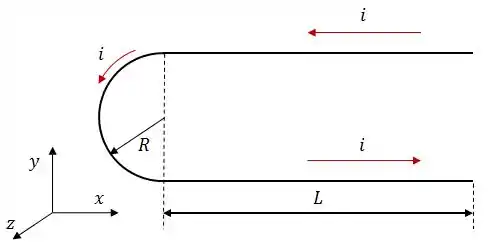
O fio está numa região onde existe um campo magnético uniforme, perpendicular ao plano do fio e orientado para fora da página, conforme figura ao lado.
- Calcule o vetor força magnética que age sobre cada fio retilíneo;
- Calcule o vetor força magnética que age sobre a parte circular;
- Calcule a força resultante que age sobre o fio todo;
Questão 6
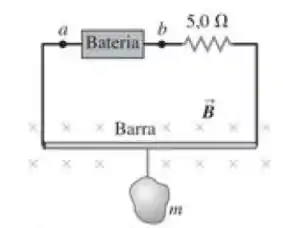
Uma barra metálica de peso , com comprimento e resistência , respousa horizontalmente sobre fios condutores do circuito indicado na Figura abaixo. A barra está em um campo magnético horizontal uniforme de e não está conectada aos fios do condutor. Qual a aceleração da barra logo após a chave ser fechada?
Questão 7
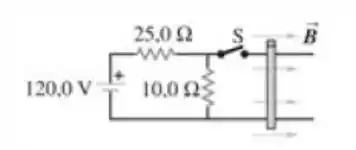
Balança magnética. O circuito da Figura abaixo é usado para produzir uma balança magnética para pesar objetos. A massa a ser medida está suspensa a partir do centro da barra, que se situa em um campo magnético uniforme de , orientado para dentro do plano da Figura. A voltagem da bateria pode ser ajustada de modo a variar a corrente no circuito. A barra condutora horizontal tem de comprimento e é feita de um material extremamente leve. Está conectada à bateria por fios verticais finos que não podem suportar nenhuma tensão considerável: todo o peso da massa suspensa é sustentado pela força magnética na barra. Um resistor de está ligado em série com a barra; a resistência do restante do circuito é muito menor que isso.
- Qual ponto, ou , deve ser o terminal positivo da bateria?
- Se a voltagem máxima do terminal da bateria é igual a , qual é a maior massa que esse instrumento pode medir?
Questão 8
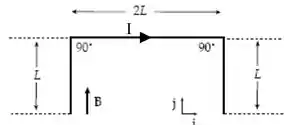
O fio dobrado da figura abaixo está submetido a um campo magnético uniforme. Cada trecho retilíneo tem de comprimento e faz um ângulo de com o eixo .
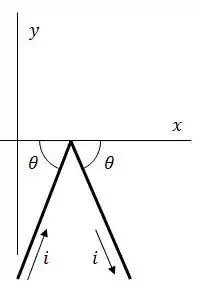
O fio é percorrido por uma corrente de . Qual é a força que o campo magnético exerce sobre o fio em termos de vetores unitários, se o campo magnético é:
;
;
Ver solução completaQuestão 9
Na figura abaixo, um fio metálico de massa pode deslizar com atrito insignificante sobre dois trilhos paralelos horizontais separados por uma distância .
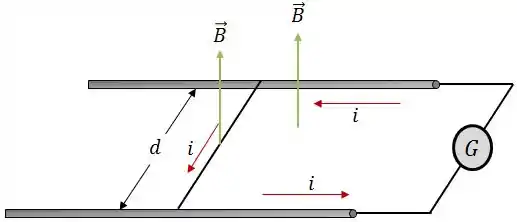
O conjunto está em uma região onde existe um campo magnético uniforme de módulo .
No instante um gerador é ligado aos trilhos e produz uma corrente constante no fio e nos trilhos (mesmo quando o fio está se movendo). No instante , determine:
a velocidade escalar do fio;
o sentido do movimento do fio (para a esquerda ou para a direita).
Ver solução completaQuestão 10
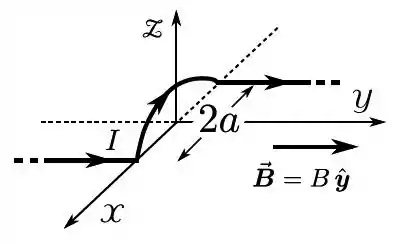
Calcule a força magnética resultante sobre o pedaço de fio, através do qual passa uma corrente elétrica estacionária de intensidade , composto por dois segmentos retilíneos, de comprimento , muito grande, e uma semicircunferência de círculo, de raio , na presença de um campo magnético constante (estacionário e uniforme) , .
Questão 11
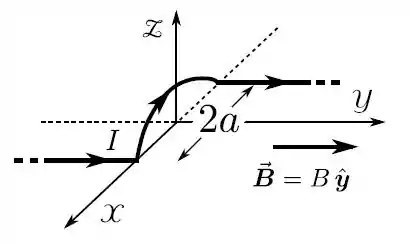
Calcule a força magnética resultante sobre o pedaço de fio, através do qual passa uma corrente elétrica estacionária de intensidade , composto por dois segmentos retilíneos, de comprimento , muito grande, e uma semicircunferência de círculo, de raio , na presença de um campo magnético constante (estacionário e uniforme) , .
Questão 12
A espira da figura, formada por dois arcos circulares de raio e dois lados retilíneos de comprimento , é percorrida por uma corrente . Um fio retilíneo muito longo transportando uma corrente passa pelo centro de curvatura dos arcos circulares (o fio não está em contato com a espira).
O módulo do campo magnético produzido pelo fio é , onde é a distância ao fio.
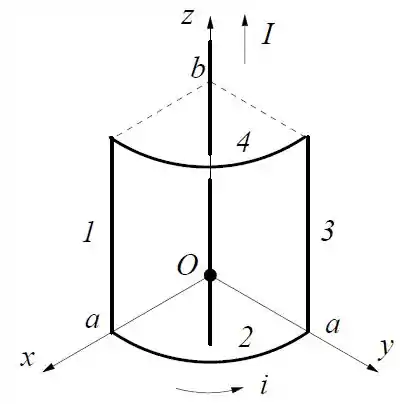
- Calcule o vetor força resultante exercida sobre cada um dos lados da espira pelo fio.
- Calcule o vetor torque resultante em relação à origem exercido sobre a espira pelo fio.
Questão 13
A figura mostra um anel circular, muito fino, de raio , submetido a um campo magnético (estacionário) divergente e com simetria radial. O campo magnético em todos os pontos do anel tem o mesmo módulo , é perpendicular ao anel e faz um ângulo com a normal ao plano do anel. Qual é a força magnética que o campo exerce sobre a espira se, nessa, passa uma corrente de intensidade ?
(a)
(b)
(c)
(d)
(e)

Questão 14
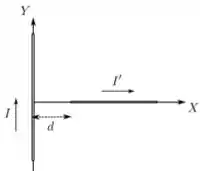
. Um fio condutor fino, retilíneo e infinito é posicionado sobre o eixo de um sistema de coordenadas. Um segundo fio condutor fino, retilíneo e finito, de comprimento , é posicionado sobre o eixo com sua extremidade mais próxima a uma distância do primeiro fio, como mostrado na figura abaixo. Os fios transportam correntes estacionárias de intensidades e nos sentidos indicados. Quais são o módulo e o sentido da força magnética resultante que o primeiro fio exerce sobre o segundo?
Dados:
Escolha uma opção:
positivo
negativo
negativo
negativo
positivo
positivo
negativo
positivo
Ver solução completaQuestão 16
1. Fios paralelos percorridos por correntes no mesmo sentido atraem-se mutuamente.
Escolha uma opção:
( ) Verdadeiro
( ) Falso
Ver solução completaQuestão 17
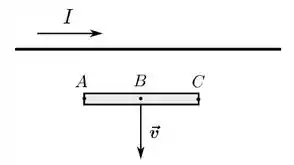
Um fio condutor fino e infinito transporta uma corrente estacionária de intensidade da esquerda para a direita, como mostrado na figura abaixo. Uma barra condutora fina desloca-se para baixo com velocidade constante de forma que seu eixo permanece paralelo ao eixo do fio, como indicado. Considere os pontos , e da barra mostrados na figura e sejam , e os potenciais elétricos nestes pontos após estabelecido o equilíbrio de cargas, respectivamente. Nessa situação, podemos afirmar que:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Ver solução completaQuestão 18
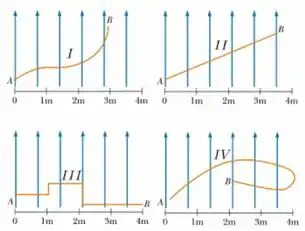
. A figura abaixo mostra quatro fios finos e condutores, e , que transportam correntes estacionárias de mesma intensidade do ponto ao ponto . Eles estão completamente imersos em um mesmo campo magnético constante que aponta para cima,
como indicado pelas setas. Dessa forma, podemos afirmar que a força magnética exercida pelo campo tem o maior módulo sobre o fio:
Não há dados suficientes para afirmar.
Ver solução completaQuestão 19
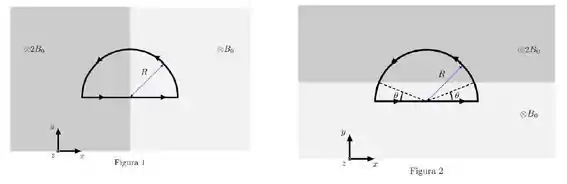
Uma espira semicircular de raio está posicionada entre duas regiões de campo magnético constante (nas Figuras 1 e 2, a região cinza-claro) e (nas Figuras 1 e 2, a região cinza-escuro). A espira é percorrida por uma correnteno sentido indicado nas Figuras 1 e 2. Observe que, na Figura 1, as metades da espira se encontram em regiões distintas. Calcule o vetor força magnética resultante na espira devido aos campos magnéticos de cada região, quando a espira se encontra:
- Posicionada como mostra a figura ;
- Posicionada como mostra a figura , onde o ângulo é .
Questão 20
3 - Os dois casos distintos representados na figura mostram duas espiras circulares, posicionadas paralelamente uma à outra, percorridas por correntes de mesma intensidade. Os sentidos das correntes estão indicados na figura. Podemos afirmar que as forças magnéticas sobre as espiras nos casos 1 e 2 são:
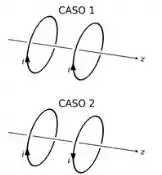
- caso 1: atrativas, caso 2: repulsivas
- caso 1: repulsivas, caso 2: atrativas
- caso 1: repulsivas, caso 2: repulsivas
- caso 1: atrativas, caso 2: atrativas
- caso 1: atrativas, caso 2: nulas
Questão 21
Dois fios paralelos e idênticos, transportam correntes e , no mesmo sentido, respectivamente. Considerando que , qual das seguintes afirmações representa a relação entre as forças magnéticas e que os respectivos fios e experimentam?
Questão 22
Parte 1: Um fio isolante infinito, alinhado com o eixo , está carregado com a densidade de carga positiva . Uma carga pontual, com valor , é colocada no ponto , sendo .
a) Calcule o campo elétrico nos pontos , sendo .
b) Encontre o valor de no qual o campo elétrico é nulo.
Parte 2: Três cargas pontuais idênticas estão situadas nos vértices de um triângulo equilátero de lado .
c) Calcule a energia eletrostática do sistema.
d) Calcule a que distância das cargas está o ponto no qual o campo elétrico é nulo.
Ver solução completaQuestão 23
Considere uma espira retangular pela qual passa uma corrente elétrica estacionária de intensidade . O sistema de eixos foi escolhido de modo que a espira se encontra no plano e o sentido da corrente na espira está indicado na figura.
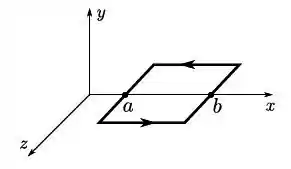
Sabe-se que o campo magnético na região onde a espira se encontra é dado por , tal que o gráfico de contra está mostrado a seguir:
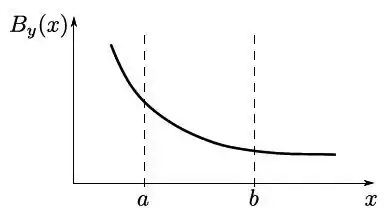
Com respeito a força magnética resultante sobre a espira, é correto afirmar que:
- Ela aponta no sentido de
- Ela aponta no sentido de
- Ela aponta no sentido de
- Ela aponta no sentido de
- Ela aponta no sentido de
- Ela aponta no sentido de
- Ela é nula
Questão 24
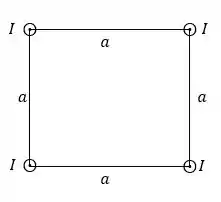
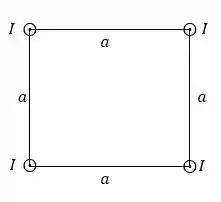
Quatro longos fios de cobre são paralelos entre si e estão dispostos em um quadrado de lado . Eles conduzem correntes iguais para fora da página, conforme mostrado na figura.
- Indique a direção e sentido da força em qualquer um dos fios. Desenhos são encorajados.
Questão 25
Quatro longos fios de cobre são paralelos entre si e estão dispostos em um quadrado de lado . Eles conduzem correntes iguais para fora da página, conforme mostrado na figura.
b) encontre a expressão literal para o módulo da força por metro sobre qualquer um dos fios. Substitua os valores para , e indique o valor da força.
Questão 26
Uma espira quadrada de lado , contida no plano , é percorrida por uma corrente no sentido horário, conforme a figura. Na região onde se encontra a espira existe um campo magnético
onde é uma constante.
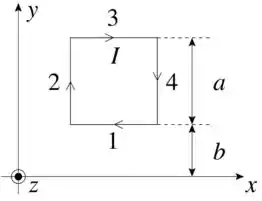
(a) Calcule a força magnética sobre os lados e da espira.
(b) Calcule a força magnética sobre os lados e da espira.
(c) Calcule a força resultante sobre a espira.
Ver solução completaQuestão 27
A figura a seguir mostra uma bateria com . Esta bateria imprime uma corrente através de um fio () de que apresenta uma resistência de . Considerando o campo magnético uniforme entre os polos do ímã e igual a , determine o módulo e a direção da força magnética que esse campo exerce sobre o trecho do fio.
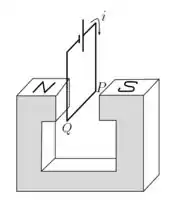
(a) para baixo da página.
(b) para cima da página.
(c) para baixo da página.
(d) para cima da página.
(e) para a esquerda.
Ver solução completaQuestão 28
Na figura abaixo o campo magnético é uniforme e perpendicular ao plano da figura, apontando para fora (direção positiva do eixo ). A espira é formada por um quarto de círculo de raio (arco ) e por dois segmentos retilíneos e de comprimento , conforme-te a figura. Pela espira circula uma corrente no sentido anti-horário.
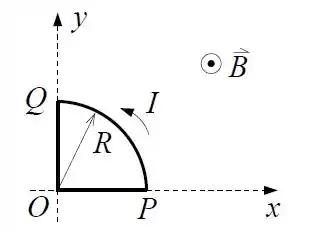
Calcule a força magnética em cada um dos três trechos , e da espira.
Ver solução completaQuestão 29
Uma espira é formada por dois segmentos de reta de comprimento e um trecho semicircular de raio , conforme ilustrado na figura. A espira está sujeita a um campo magnético uniforme dado por e a corrente percorre a espira no sentido indicado na figura.
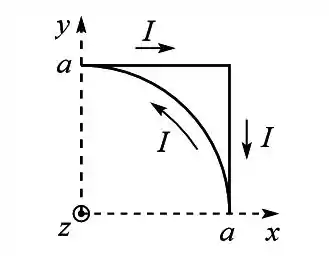
(a) Calcule o vetor força magnética sobre os segmentos retilíneos horizontal e vertical.
(b) Calcule o vetor força magnética sobre o trecho circular.
Ver solução completaQuestão 30
Um fio condutor, curvado na forma de um semicírculo de raio , forma um circuito fechado e é percorrido por uma corrente . O circuito está no plano e um campo magnético uniforme está aplicado paralelamente ao eixo , com é visto na figura.
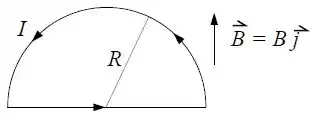
Determine a força magnética total (vetor) sobre a parte retilínea do condutor.
Determine a força magnética total (vetor) sobre a parte curva do condutor.
Ver solução completaQuestão 31
A figura abaixo mostra um fio que conduz uma corrente . Ele é formado por dois trechos retilíneos de comprimento , ambos tangentes à mesma circunferência de raio , e por um arco desta circunferência que subentende um ângulo central de , conforme a figura abaixo.
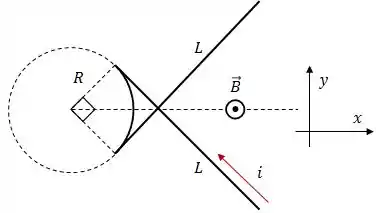
O fio está numa região onde existe um campo magnético uniforme, perpendicular ao plano da página e orientado para fora dela.
Calcule o vetor força magnética que age sobre cada segmento de fio retilíneo;
Calcule o vetor força magnética que age sobre a parte circular;
Calcule a força resultante que age sobre o fio;
Ver solução completaQuestão 32
(Capítulo 28.9 – Exercício 49) A Fig. 28-44 mostra uma bobina retangular de cobre, de 20 espiras, com de altura e de largura. A bobina conduz uma corrente de e dispõe de uma dobradiça em um dos lados verticais. Está montada no plano xy, fazendo um ângulo com a direção de um campo magnético uniforme de módulo . Em termos dos vetores unitários, qual é o torque em relação à dobradiça que o campo exerce sobre a bobina?
Ver solução completaQuestão 33
(Capítulo 28 – Problemas Adicionais – Exercício 67) Um relógio de parede estacionário tem um mostrador circular com de raio. Seis espiras de fio são enroladas no mostrador; o fio conduz uma corrente de no sentido horário. No local onde o relógio se encontra existe um campo magnético uniforme de (que não impede o relógio de mostrar corretamente a hora).
Exatamente às 13 h, o ponteiro das horas do relógio aponta na direção do campo magnético. (a) Após quantos minutos o ponteiro de minutos do relógio aponta na direção do torque exercido pelo campo magnético sobre a bobina? (b) Determine o módulo do torque.
Ver solução completaQuestão 34
Temos um circuito condutor na forma de triângulo equilátero de lado , ao longo do qual flui uma corrente elétrica estacionária de intensidade e sentido como representado na figura abaixo. Tal circuito está sujeito a um campo magnético constante (estacionário e uniforme) , com sentido indicado na figura. Marque a opção que melhor corresponde à força magnética resultante sobre o circuito.
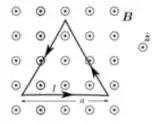
a)
b)
c)
d)
e)
Ver solução completaQuestão 35
Um fio condutor, retilíneo, muito longo transporta uma corrente estacionária de intensidade no sentido indicado na figura.
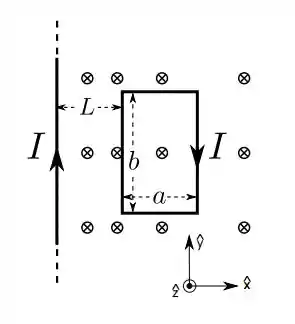
Uma espira retangular, coplanar com o fio, de lados (horizontal) e (vertical) se encontra, em repouso, a uma distância à direita do fio. Através desta espira circula uma corrente no sentido horário. Qual a direção e o sentido da força magnética resultante sobre a espira?
(a)
(b)
(c)
(d)
(e)
(f)
Ver solução completaQuestão 36
A borda direita do circuito da figura estende-se para dentro de uma região com um campo magnético uniforme de .
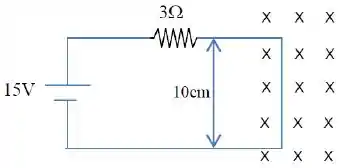
A intensidade e a orientação da força resultante sobre o circuito respectivamente são iguais a:
, saindo da página.
, dirigida para a direita.
, dirigida para a direita.
, dirigida para a direita.
, saindo da página.
Ver solução completaQuestão 37
(Capítulo 28.8 – Exercício 45) Um fio de 50,0 cm de comprimento é percorrido por uma corrente de 0,500 A no sentido positivo do eixo x na presença de um campo magnético . Em termos dos vetores unitários, qual é a força que o campo magnético exerce obre o fio?
Ver solução completaQuestão 38
(Capítulo 28.8 – Exercício 47) Uma barra de cobre de 1,0 kg repousa em dois trilhos horizontais situados a 1,0 m de distância um do outro e é percorrida por uma corrente de 50 A. O coeficiente de atrito estático entre a barra e trilhos é 0,60. Determine (a) o módulo e (b) o ângulo (em relação à vertical) do menor campo magnético que faz a barra se mover.
Ver solução completaQuestão 39
Considere uma espira quadrada de lado percorrida por uma corrente . A espira se encontra no plano , conforme a figura.
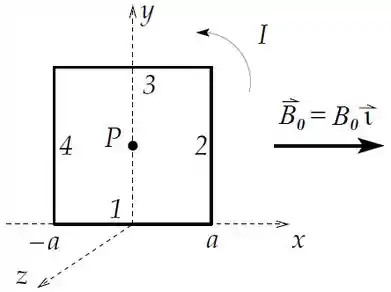
Calcule as forças resultantes e exercidas pelo campo externo sobre cada um dos lados do quadrado.
Ver solução completaQuestão 40
Um fio fino, transportando uma corrente , é dobrado na forma de um grampo composto por dois segmentos retilíneos de comprimento e um arco semicircular de raio .
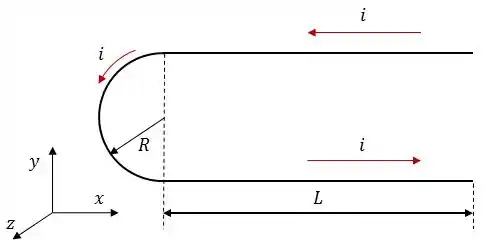
O fio está numa região onde existe um campo magnético uniforme, perpendicular ao plano do fio e orientado para fora da página, conforme figura ao lado.
- Calcule o vetor força magnética que age sobre cada fio retilíneo;
- Calcule o vetor força magnética que age sobre a parte circular;
- Calcule a força resultante que age sobre o fio todo;
Questão 41
Uma corrente flui no sentido anti-horário pelo contorno desta página e um campo magnético uniforme está dirigido da esquerda para a direita, paralelamente ao plano da página.
Se a força magnética é a única que age na região, a página girará de modo que a margem direita:
move-se em sua direção;
move-se para a sua direita;
move-se para a sua esquerda;
move-se afastando-se de você;
não se move;
Ver solução completaQuestão 42
Uma barra de comprimento e resistência desliza, sem atrito, sobre um trilho inclinado por um ângulo de . O conjunto está em um campo magnético , com linhas de campo verticais direcionadas para baixo. A barra é solta a partir do repouso de uma certa altura no trilho e começa a deslizar devido ao seu peso . Qual é o valor da velocidade terminal?
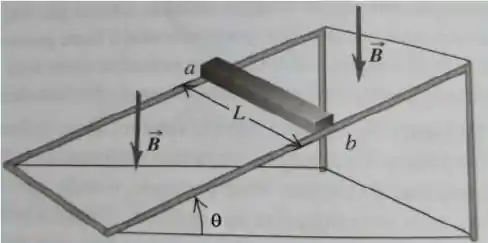
Questão 43
Uma espira condutora quadrada de lado é posicionada sobre o plano de um sistema de coordenadas como mostrado na figura abaixo. Seus lados são paralelos aos eixos e um de seus vértices está sobre a origem. Ela transporta uma corrente estacionária de intensidade e sentido anti-horário e está imersa em uma região de campo magnético estacionário, mas não-uniforme dado por, onde é uma constante positiva. Sobre essa situação, é CORRETO afirmar que a força magnética resultante sobre a espira:
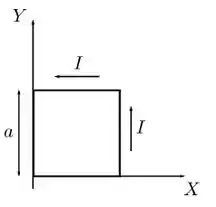
(a) Aponta no sentido
(b) Aponta no sentido
(c) Aponta no sentido
(d) Aponta no sentido
(e) Aponta no sentido
(f) Aponta no sentido
(g) É nula.
Ver solução completaQuestão 44
Uma fita metálica de largura conduz uma corrente . Portanto, a densidade superficial de corrente é
- Se tivermos uma partícula de carga , positiva, com velocidade se movendo em uma direção ortogonal ao plano da fita, se aproximando da fita e muito próxima a ela, qual será o módulo da força magnética que age sobre a partícula?
- Descreva o sentido da força do item (b)
Questão 45
A figura abaixo mostra três fios que conduzem correntes da mesma intensidade do ponto ao . O fio é formado por dois segmentos de reta inclinados de mesmo comprimento, o fio é um único segmento de reta horizontal de comprimento e o fio é um semicírculo de diâmetro . O segmento de reta tracejado na figura tem comprimento . Os fios estão numa região de campo magnético constante perpendicular ao plano da página, com sentido para dentro. Sejam , e as intensidades das forças magnéticas que o campo exerce sobre os fios , e respectivamente. Nessas condições, podemos afirmar que:
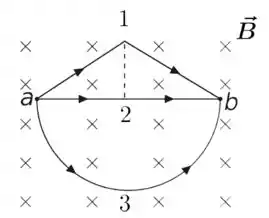
Questão 46
A figura ilustra uma bobina com espiras circulares enroladas em uma solenóide de comprimento e raio . A corrente elétrica que circula na bobina produz um campo magnético de magnitude igual a próximo ao centro da bobina. A intensidade da corrente é (use ):
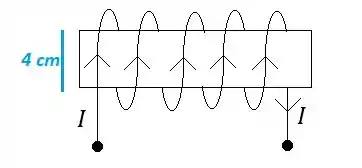
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 47
Uma espira retangular de lados e é colocada em duas regiões: a superior com campo magnético e a inferior com como mostra a figura ao lado. A espira é percorrida por uma corrente de intensidade no sentido apresentado na figura.
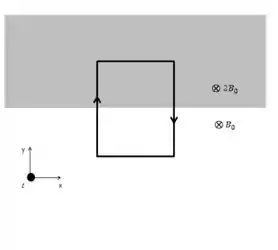
a) Qual deve ser a massa da espira (preste atenção no sentido da gravidade na figura) para que ela fique suspensa no ar?
b) Qual deve ser o novo valor da massa para que a espira permaneça em equilíbrio quando mudamos sua orientação para a mostrada na figura inferior?
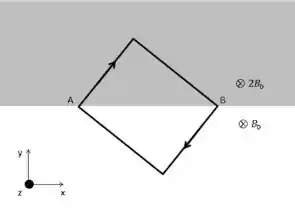
Questão 48
Um condutor formado por dois segmentos condutores retilíneos ortogonais de comprimentos e é percorrido por uma corrente constante , conforme a figura.
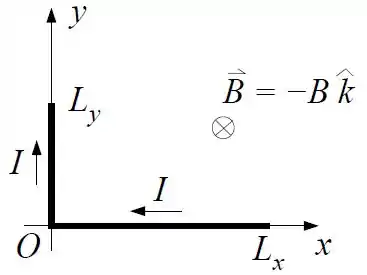
Um campo magnético constante uniforme é aplicado perpendicularmente ao plano para dentro da figura.
Calcule o vetor força exercida por sobre o trecho ?
Calcule o vetor força exercida por sobre o trecho ?
Ver solução completaQuestão 49
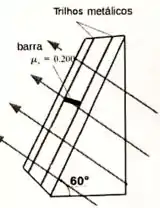
3 – Uma barra de metal de comprimento tem uma massa com suas extremidades apoiadas sobre trilhos metálicos. Os trilhos estão fixados sobre um plano inclinado que forma um ângulo com a horizontal. Os trilhos têm resistência elétrica desprezível, comparada à resistência da barra. Existe um campo magnético perpendicular à superfície inclinada em toda a região dos trilhos (ver figura abaixo). Os dois pontos de apoio nas extremidades da barra, em contato com os trilhos metálicos, permitem a passagem de corrente elétrica através da barra. Fecha-se o circuito com uma fonte de tensão ajustável conectada aos trilhos (fonte não representada na figura). O coeficiente de atrito estático entre a barra e os contatos é de . Quais as magnitudes e direções, mínima e máxima, da corrente que deve passar pela barra para impedir que ela se mova?
Dica: A força de atrito estático tem como módulo o valor máximo , onde é o modulo da força normal da superfície.
Questão 50
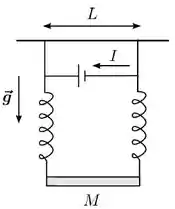
Uma barra metálica de comprimento e massa encontra-se suspensa por meio de molas metálicas ideais presas ao teto, como mostrado na figura abaixo. As molas estão conectadas por uma bateria que fornece uma corrente estacionária de intensidade no sentido indicado. Deseja-se então aplicar um campo magnético uniforme e estacionário sobre esse sistema de forma que a barra fique suspensa sem que haja nenhuma tensão sobre as molas. Sabendo que o módulo da aceleração da gravidade local vale , podemos afirmar que o módulo, direção e sentido deste campo magnético são, respectivamente:
(a) , perpendicular ao plano do papel e apontando para dentro.
(b) , perpendicular ao plano do papel e apontando para fora.
(c) , perpendicular ao plano do papel e apontando para dentro.
(d) , perpendicular ao plano do papel e apontando para fora.
(e) , no plano do papel, apontando para cima.
(f) , no plano do papel, apontando para baixo.
(g) , no plano do papel, apontando para cima.
(h) , no plano do papel, apontando para baixo.
Ver solução completaQuestão 51
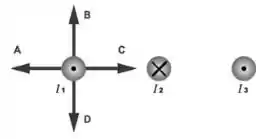
8 - A figura mostra três longos fios paralelos transportando corrente. As magnitudes das correntes são iguais () e seus sentidos estão indicados na figura. Qual das setas desenhadas melhor representa o sentido da força magnética que atua sobre o fio de corrente ?
- A
- B
- C
- D
- A força magnética na corrente é igual a zero.
Questão 52
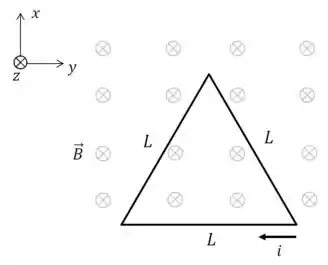
Um circuito que tem o formato de um triângulo equilátero de lado , está no plano e é percorrido por uma corrente constante, no sentido horário. O circuito está imerso em um campo magnético na direção (entrando na folha, como mostra a figura).
a) Mostre a direção e sentido da força magnética atuando em cada lado do circuito, através de um diagrama.
b) Calcule o módulo da força magnética em cada lado do triângulo.
c) Calcule o momento magnético do circuito.
d) Calcule o torque inicial sobre o circuito.
Ver solução completaQuestão 53
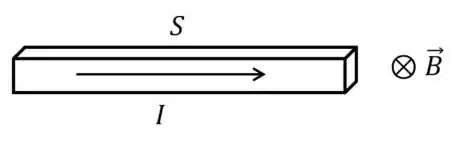
A figura mostra um condutor com uma corrente que flui da esquerda para a direita, imerso em um campo magnético dirigido para “dentro” da página. A superfície (superior) está a um potencial maior que a superfície (inferior). Os portadores de carga:
a) são negativos
b) são positivos
c) são neutros
d) são ausentes
e) movem-se com velocidade próxima à da luz
Ver solução completaQuestão 54
Uma chapa isolante e infinita de espessura é posicionada paralelamente ao plano de um sistema de coordenadas, como mostrado na figura abaixo. O plano central desta chapa coincide com este plano. A chapa encontra-se carregada com uma densidade volumétrica de carga constante e positiva . Sobre esse sistema, é CORRETO afirmar que:
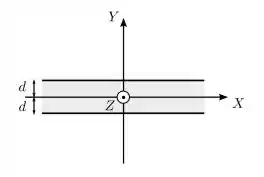
- O campo elétrico produzido pela chapa é nulo em todos os pontos do plano XZ.
- O campo elétrico produzido pela chapa tem o mesmo sentido em todos os pontos do espaço.
- O campo elétrico produzido pela chapa é uniforme em todos os pontos na região dentro da chapa.
- O potencial elétrico produzido pela chapa tem o mesmo valor todos os pontos na região fora da chapa.
- O potencial elétrico produzido pela chapa tem o mesmo valor em todos os pontos na região dentro da chapa.
Questão 55
Duas partículas de cargas e são fixadas sobre o eixo de um sistema de coordenadas nos pontos e , respectivamente (). Em que ponto desse eixo deve ser posicionado uma terceira partícula de carga de forma que ela fique em equilíbrio?
Questão 56
Dois fios finos, retilíneos e infinitos são posicionados sobre os eixos X e Y de um sistema de coordenadas cartesianas, como mostrado na figura abaixo.
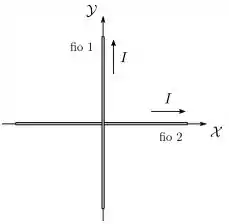
Os fios transportam correntes estacionárias de mesma intensidade , nos sentidos indicados. Nessas condições, podemos afirmar que a força resultante que o fio 1 (vertical) exerce sobre o fio 2 (horizontal):
- é nula.
- aponta no sentido .
- aponta no sentido .
- aponta no sentido .
- aponta no sentido .
- aponta no sentido .
- aponta no sentido .
Questão 57
Três fios condutores finos, retilíneos e infinitos são alinhados paralelamente. Eles cruzam os vértices de um triângulo equilátero de lado , de forma que o plano deste triângulo é perpendicular aos eixos dos fios. A situação é mostrada na figura abaixo, onde os fios são designados por 1, 2 e 3. Ao medir-se a força magnética resultante por unidade de comprimento sobre o fio 1, obtém-se o vetor indicado na figura. Sabendo que os três fios são atravessados por correntes estacionárias, considere as afirmativas abaixo:
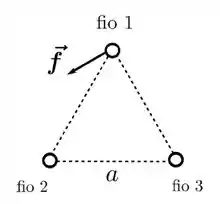
(I) As correntes que atravessam os fios 1 e 3 têm o mesmo sentido.
(II) As correntes que atravessam os fios 2 e 3 têm sentidos opostos.
(III) A corrente que atravessa o fio 2 tem intensidade maior que aquela que atravessa o fio 3.
São VERDADEIRAS as afirmativas:
(a) Apenas II e III
(b) Apenas I
(c) Apenas II
(d) Apenas III
(e) Apenas I e II
(f) Apenas I e III
(g) I, II e III
(h) Nenhuma delas
Ver solução completaQuestão 58
2.7) Considere um fio cilíndrico longo de raio conduzindo uma corrente distribuída uniformemente ao longo de sua secção transversal. Determine a dependência do módulo do
vetor campo magnético com a distância medida a partir do eixo central do fio.
Ver solução completaQuestão 59
2.10) Considere um fio cilíndrico infinito de raio conduzindo uma corrente distribuída
uniformemente ao longo da seção transversal. Quais são as duas distâncias ao eixo do fio
para as quais a intensidade do campo magnético, devido à corrente, é igual à metade do
valor na superfície?
Ver solução completa