Na figura abaixo, duas partículas pontuais, de massas distintas e , e cargas elétricas idênticas e positivas de valor , deslocam-se ao longo do eixo com velocidades constantes dadas por .
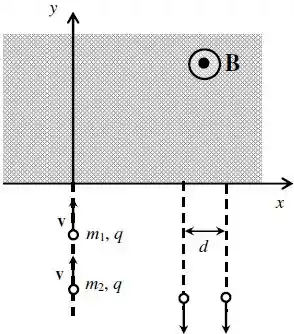
Tais partículas penetram a região , onde existe um campo magnético uniforme , perpendicular ao plano e saindo do plano da página.
Considere que o campo magnético é nulo fora da região . Sabe-se que, ao saírem da região , as partículas movem-se em trajetórias retilíneas e paralelas entre si.
Calcule o comprimento das trajetórias descritas pelas partículas, na região .
Calcule o trabalho realizado pela força magnética sobre as partículas, durante o deslocamento das mesmas na região .
Neste item, assuma que , e que é conhecida, enquanto que é desconhecida. Sabe-se também que as partículas, ao saírem da região , cruzam o eixo separadas por uma distância (veja figura). Nestas circunstâncias, calcule o valor da massa desconhecida , em função das grandezas conhecidas , , , e .
Passo 1
Calcule o comprimento das trajetórias descritas pelas partículas, na região .
Ao entrar na região com campo magnético, as partículas irão descrever trajetórias circulares, cujo raio é dado por:
No entanto, como o campo magnético está presente somente na região . As partículas irão descrever uma semicircunferência.
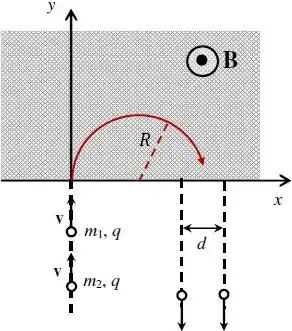
Nesse caso, o comprimento da trajetória será:
Para cada partícula, teremos:
Passo 2
Calcule o trabalho realizado pela força magnética sobre as partículas, durante o deslocamento das mesmas na região .
Tá aí uma coisa que você precisa ter sempre em mente, beleza?!
A força magnética não realiza trabalho!
Logo, .
Mas como assim ela não realiza trabalho?
Como a trajetória da partícula é circular, o trabalho infinitesimal sobre um pedaço da trajetória, de tamanho , é dado por:
Onde:
Logo:
O produto vetorial irá nos dar um vetor que é perpendicular a . Logo, o produto escalar, que é realizado em seguida, entre dois vetores perpendiculares é nulo.
Finalmente:
Passo 3
Neste item, assuma que , e que é conhecida, enquanto que é desconhecida. Sabe-se também que as partículas, ao saírem da região , cruzam o eixo separadas por uma distância (veja figura). Nestas circunstâncias, calcule o valor da massa desconhecida , em função das grandezas conhecidas , , , e .
Aqui, a distância representa a diferença entre os diâmetros das suas partículas.
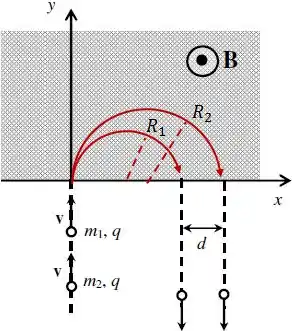
Substituindo as expressões dos raios, teremos:
Todas as variáveis que precisamos estão aqui. Agora é só dar aquela arrumada.
Resposta