Na figura abaixo, uma partícula (que pode ser um próton ou um elétron) descreve uma trajetória circular em uma região onde existe um capo magnético uniforme de módulo igual a (saindo do plano do papel). A partícula está sujeita a uma força magnética de módulo igual a .

Identifique o sinal da carga da partícula (justifique);
Determine:
A velocidade escalar da partícula;
O raio da trajetória da partícula;
O período do movimento;
Dados:
massa do próton:
massa do elétron:
Passo 1
Identifique o sinal da carga da partícula (justifique);
Para que a partícula esteja percorrendo a trajetória da figura, é necessário que a força magnética sobre ela faça o papel de força centrípeta, apontando para dentro da trajetória.
A força magnética sobre uma partícula é dada por:
Assim, o sentido da força é determinado pela regra da mão direita.
De acordo com a figura, o produto vetorial entre e aponta no sentido oposto ao do centro da circunferência.
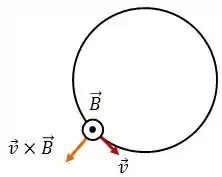
Assim, para que a força magnética aponte para o centro da circunferência, a carga deve ser negativa, ou seja, um elétron.
Passo 2
A velocidade escalar da partícula;
De acordo com o problema:
Sabendo que a carga de um elétron é , a velocidade é dada por:
Passo 3
O raio da trajetória da partícula;
Como a força magnética faz o trabalho de força centrípeta, podemos igualá-las:
Substituindo os valores:
Passo 4
O período do movimento;
O período pode ser determinado por:
Substituindo os valores:
Resposta
A carga é um elétron.