Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Raio e Intervalo de Convergência

Ver Teoria
Exercício 361234567891011121314151617181920212223242526272829303132333435373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

IME, Cálculo 3, 2021, VE2, Q4

Determine o conjunto de valores de x para o qual a série ∑ n = 0 ∞ - 2 n n + 2 n + 1 x n ,     x ∈ R , converge.

Passo 1

Falem, meus amores. Nos últimos anos, as províneas do IME pelo que dizem pedem análise de convergência pontual, uniforme, absoluta e condicional. Com séries de potências a análise fica mais fácil, pois temos o conceito de círculo de convergência. Começamos determinando-o e depois analisamos sua borda. Séries de potências de base x real na forma:

  ∑ n = 0 ∞ a n ( x - x 0 ) n

São tais que convergem absolutamente no interior de um “círculo” [ x 0 - r ,   x 0 + r ] (nesse caso um intervalo) ao qual chamamos de círculo de convergência e divergem em seu exterior como abaixo:

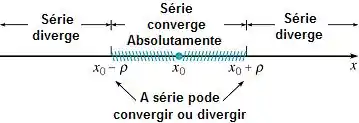
Onde x 0 é o centro do círculo e r é seu raio. Em nossa série, observe em primeiro lugar que x 0 = 0 . Para averiguarmos a divergência utilizaremos o Teste da Razão. Este afirma que dada uma série ∑ n = 0 ∞ b n :

L = lim n → ∞ ⁡ b n + 1 b n

Temos que:

s e   L < 1 ,   a   s é r i e   c o n v e r g e       s e   L = 1 ,   o   t e s t e   é   i n c o n c l u s i v o s e   L > 1 ,   a   s é r i e   d i v e r g e

Assim, para x ≠ 0 :

lim n → ∞ ⁡ b n + 1 b n = lim n → ∞ ⁡ a n + 1 x n + 1   a n   x n =

= lim n → ∞ ⁡ 2 n + 3 n + 1 n + 2 2 | x | = lim n → ∞ ⁡ 2 1 + 3 n 1 + 1 n 1 + 2 n 2 | x | = 2 | x |

Logo, o limiar que marca a mudança de convergência é dado por:

2 x = 1 ⇒ x = ± 1 2  

Assim, o raio de convergência é 1/2. Determinado o círculo de convergência devemos analisar o limiar.

Passo 2

Portanto, para x = - 1 / 2 :

  ∑ n = 0 ∞ - 2 n n + 2 n + 1 x n =   ∑ n = 0 ∞ - 2 n n + 2 n + 1 - 1 2 n =   ∑ n = 0 ∞ n + 2 n + 1

Cujo termo geral, não converge para 0 no infinito e como

lim n → ∞ ⁡ a n ≠ 0 ⇒ a   s é r i e   d i v e r g e

a série diverge nesse ponto. Contudo, para x = 1 / 2 :

∑ n = 0 ∞ - 2 n n + 2 n + 1 x n =   ∑ n = 0 ∞ - 2 n n + 2 n + 1 1 2 n =   ∑ n = 0 ∞ - 1 n n + 2 n + 1

Assim, observe que o módulo do termo desta se iguala ao caso anterior, logo a série dos módulos diverge (série não converge absolutamente). A série em si é tal que tomando os termos dois a dois:

∑ n = 0 ∞ - 1 n n + 2 n + 1 = ∑ k = 0 ∞ - 1 2 k 2 k + 2 2 k + 1 + - 1 2 k + 1 2 k + 1 + 2 2 k + 1 + 1

= ∑ k = 0 ∞ 2 k + 2 2 k + 1 - 2 k + 3 2 k + 2 = ∑ k = 0 ∞ 2 k + 2 2 - 2 k + 1 2 k + 3 2 k + 1 2 k + 2 =

= ∑ k = 0 ∞ 4 k 2 + 8 k + 4 - 4 k 2 + 8 k + 3 2 k + 1 2 k + 2 = ∑ k = 0 ∞ 1 2 k + 1 2 k + 2

a qual converge, uma vez que séries da forma:

∑ k = 0 ∞ 1 k p

convergem desde que p > 1 e divergem quando 0 < p ≤ 1 . Assim, para x = 1 2 a série converge condicionalmente, uma vez que a série de termos converge e a série do módulo dos termos diverge.

Passo 3

Assim, a série, segundo teoremas:

  • DIVERGE em ] - ∞ , - 1 2 [     ∪     ] 1 2 , ∞ [   (exterior)
  • CONVERGE ABSOLUTAMENTE, UNIFORMEMENTE E PONTUALMENTE em ] - 1 2 , 1 2 [   (interior)

    • E ainda,

    • DIVERGE em x = - 1 / 2
    • CONVERGE CONDICIONALMENTE, UNIFORMEMENTE E PONTUALMENTE em x = 1 / 2

      • Resposta

      Assim, a série, segundo teoremas:

    • DIVERGE em ] - ∞ , - 1 2 [     ∪     ] 1 2 , ∞ [   (exterior)
    • CONVERGE ABSOLUTAMENTE, UNIFORMEMENTE E PONTUALMENTE em ] - 1 2 , 1 2 [   (interior)

    E ainda,

  • DIVERGE em x = - 1 / 2
  • CONVERGE CONDICIONALMENTE, UNIFORMEMENTE E PONTUALMENTE em x = 1 / 2

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Suponha que a série de potências ∑ c n x - a n satisfaça c n ≠ 0 para todo n . Mostre que, se l i m n → ∞c n c n + 1 existir, então ele será igual ao raio de convergência da série de potências.
Encontre o raio de convergência e o intervalo de convergência da série: ∑ n = 1 ∞ - 2 n x n n 4
Encontre o raio de convergência e o intervalo de convergência da série. ∑ n = 0 ∞ - 1 n x - 3 n 2 n + 1
Encontre o raio de convergência e o intervalo de convergência da série: ∑ n = 1 ∞ n 2 x n 2 ∙ 4 ∙ 6 ∙ … ∙ ( 2 n )
Encontre o raio de convergência e o intervalo de convergência da série: ∑ n = 2 ∞ - 1 n x n 4 n ln ⁡ n