Uma janela tem a forma de um retângulo sob uma semicircunferência. Para um perı́metro de 5

metros, encontre as dimensões de tal janela de forma que ela admita a maior quantidade possı́vel

de luz.

Eaew, belezinha?

A questão nos pede para encontrar as dimensões de uma janela que consiste de um retângulo sob uma semicircunferência, como ilustrado na figura abaixo:

Como queremos que a janela admita a maior quantidade de luz possível, queremos construí-la tal que sua área seja a maior possível, mas com um perímetro definido de 5m. Bem, da imagem, vemos que o perímetro P(R,x) da janela é composto pelo perímetro da semicircunferência mais 3 lados do retângulo: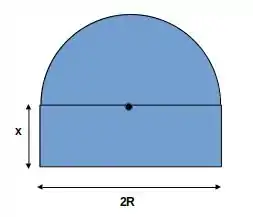

A área A(R,x) da janela, por sua vez, vai ser dada pela soma da área do retângulo e do semicírculo:

A gente vê, então, que a área total da janela depende de duas variáveis: do raio da semicircunferência e da altura do retângulo. No entanto, podemos nos livrar de uma dessas variáveis através do vínculo dado pelo perímetro, que tem um valor definido. Da relação do perímetro, obtemos

Substituindo na expressão para a área, temos:

Agora, temos uma expressão para a área que só depende de uma variável e queremos determinar qual deve ser o valor dessa variável para que a área seja máxima. Bem, a gente sabe que em um ponto de extremo de uma função, a sua derivada é nula. Então, para descobrir qual deve ser o tamanho do raio para que a área seja máxima, só precisamos derivar a função A(R) em relação à R e igualar a zero! Então vamos lá derivar!