Seja uma função de classe qualquer, definida em todo o . Assinale todas as afirmações falsas.
Escolha uma ou mais:
c. Se para todo , então
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma função e disse que se a derivada parcial dessa função em relação a for positiva, , então . Será que isso é verdade?
Bom, pela propriedade de derivadas em funções de classe 2, o sinal da derivada de em garante o crescimento somente em direções paralelas a esse eixo, porque a derivada parcial está relacionada à inclinação do gráfico de em relação a um eixo, certo? Por exemplo, se a gente tivesse uma parábola:
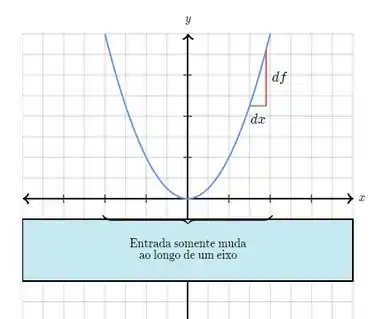
O realiza uma pequena alteração em , então a gente não pode garantir que .
Vamos testar uma função pra ficar mais claro!
Passo 2
Pegando uma função qualquer . Vamos aplicar um ponto qualquer , como na nossa alternativa:
Aplicando um ponto qualquer onde (a derivada da função em , ou ).
Ao aplicarmos um , temos:
Logo,
Comprovando que pode ser menor que. Portanto, nossa alternativa é falsa, porque provamos pelo menos 1 caso onde não acontece.
É isso, galera! Encerramos o exercício! 😉