Seja
1. é contínua em ? E em ? Justifique.
2. Calcule, se existir, e .
Passo 1
(a) Então pessoal, esse problema é presença garantida nas provas de cálculo 2. Vamos ver como a gente pode resolver.
Direto ao ponto: como a gente pode mostrar que essa função é contínua em um ponto ? Se essa condição aqui for verdadeira:
Então a função é contínua. Ou seja, se o limite da função tendendo ao ponto for igual ao valor da função naquele ponto, então ela é contínua ali.
Passo 2
No nosso caso, queremos considerar o ponto . O valor da função nesse ponto é:
Isso já é dado na definição da função! Agora vamos calcular o limite quando a função tende a esse ponto, ou seja, , mas nunca sendo exatamente igual a .
Então o limite fica assim:
Geralmente, quando a gente trabalha com limites de duas variáveis, uma boa forma de resolver é mostrar que o limite não existe.
Uma forma de fazer isso é provando que, tomando caminhos diferentes até o ponto , o limite tem valores diferentes.
Passo 3
Por exemplo, a gente pode chegar até o ponto passando por uma reta :
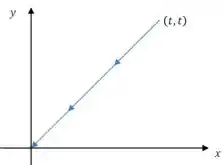
Nesse caso, os pontos da reta sempre podem ser escritos na forma .
Substituindo isso no limite:
Beleza, então tomando esse caminho o limite dá zero.
Agora vamos chegar até o ponto passando pelo eixo horizontal:
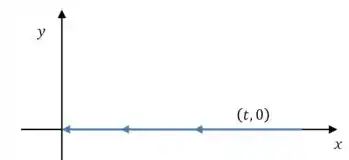
Nesse caso os pontos da reta sempre podem ser escritos como :
Dessa vez o limite deu ! Isso quer dizer que o limite não existe nesse ponto, e então essa condição aqui:
Não pode ser satisfeita! E a função não é contínua no ponto .
Passo 4
Ok, mas e o ponto ? De novo, se ela for contínua nesse ponto, vai satisfazer essa igualdade aqui:
O valor da função nesse ponto é:
E agora vamos calcular o limite:
Aqui dá pra substituir direto sem problema nenhum!
Beleza, então a condição foi satisfeita!
E então a função é contínua no ponto .
Passo 5
(b) Ok, agora vamos calcular e . Antes de começarmos a calcular, importante lembrarmos que teremos que derivar a nossa função pela definição! “Mas por quê?” Bom, se a gente for reparar no nosso enunciado, a nossa função assume valor igual a 0 quando , e a gente não pode simplesmente derivar o 0.
Se você não lembra de como fazer a derivada pela definição, fica tranquilo que eu vou te mostrar as fórmulas e como calcular:
Passo 6
Então vamos la, vamos começar pela :
Ok, chegamos numa forma bem mais simples de calcular em comparação com aquela que começamos né? E o que faremos agora? Bom, você concorda comigo que pode ser aproximar de 0 tanto pela esquerda quanto pela direita
O que isso nos lembra? Limites laterais la do nosso querido Cálculo 1! Então, vamos la:
Opa, o que temos aqui? Limites laterais diferentes, ou seja, o nosso limite não existe!
Com isso, podemos concluir que não existe!
Passo 7
Show, agora vamos calcular :
Opa, conseguimos calcular o nosso limite e encontramos um valor para ele.
Com isso, podemos concluir que = 0.
Resposta
1. A função não é contínua em , pois o seu limite tendendo a esse ponto não existe. A função é contínua em , pois .
2. não existe.
= 0.