Considere quatro cargas pontuais colocadas nos vértices de um quadrado de lado como mostrado na figura abaixo.
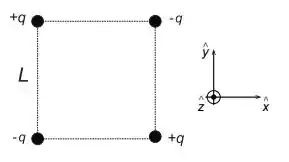
Calcule:
A força sobre a carga situada no vértice superior direito.
Passo 1
Fala aí galerinha, tudo na paz com vocês?
Nessa questão temos uma distribuição de partículas pontuais nos vértices de um quadrado de lado .
Precisamos calcular a força resultante sobre a carga no vértice superior direito do quadrado.
Para calcular a força resultante, precisamos calcular a força que cada uma das outras cargas efetua no vértice superior direito, e depois é só somar vetorialmente.
Beleza?

A força entre duas partículas pontuais, pela lei de Coulomb vale:
Show de bola! Então vamo nessa!
Passo 2
Pra começar, vamos numerar os vértices pra facilitar a indicação da força que estamos trabalhando:
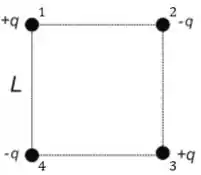
Daí, vamos iniciar calculando a força que a partícula faz em.
Como temos cargas opostas, é uma força horizontal de atração, que pelo sistema de eixos dado no enunciado pode ser expressa como:
Agora vamos calcular a força elétrica que a partícula faz em . Também é uma força de atração, mas na direção vertical. Logo:
Por fim, vamos calcular a força entre as partículas e . Aqui a força será de repulsão e irá apontar na direção da diagonal do quadrado. Assim, vamos decompô-la na direção e na direção .
Como o ângulo da diagonal do quadrado tanto com a vertical como com a horizontal é de , teremos:
Perfeito!
Passo 3
Agora que já calculamos a força que cada uma das partículas executa na partícula , para calcular a força resultante basta somar. Temos:
Prontinho pessoal! Com isso terminamosss!!
Curtiram? Responde Aí!