Calcule , o limite, quando existir. Caso contrário, justifique.
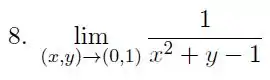
Passo 1
Vamos começar tentando substituir o ponto :
Opa, temos uma parada constante no numerador e o denominador indo pra zero.
Isso só pode ser uma indeterminação.
Mas essa indeterminação a gente já sabe pra onde vai: pro infinito.
Isso significa então que nosso limite não existe.