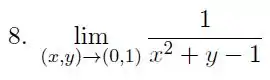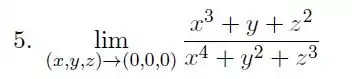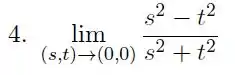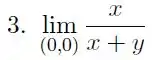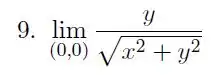Exercícios de Mostrar que o Limite Não Existe em Funções de Várias Variáveis - Lista de Exercícios Resolvida
Questão 7
Considere os seguintes limites
- existe; não existe
- existe; existe
- não existe; existe
- não existe; não existe
- Nenhuma das outras alternativas
Questão 10
Determine o limite, se existir, ou mostre que o limite não existe (Justifique!)
Ver solução completaQuestão 11
Responda os itens a seguir.
Mostre que
não existe (Não usar coordenadas polares).
Ver solução completaQuestão 12
Seja
Então, o limite
- Existe e vale
- Existe e vale
- Não existe
- Existe e vale
Questão 14
Considere a função
- Determine o domínio de
- Calcule, ou mostre que não existe, o limite de quando tende a
Questão 15
Considere os seguintes limites:
- existe; existe
- não existe; existe
- existe; não existe
- não existe; não existe
Questão 16
Considere a função
- Determine e esboce o domínio de
- Determine as curvas de nível e de , esboçando-as na mesma figura de .
- Existe ? Justifique.
Questão 23
Considere a função de duas variáveis:
1. Qual domínio dessa função? Descreva-o algebricamente e também faça um esboço.
2. Calcule, se existir, o limite abaixo. Caso nã exista, justifique.
Ver solução completaQuestão 24
Seja um parâmetro real, e seja a função seguinte:
Calcule para que valores de existe o limite:
Ver solução completaQuestão 25
Mostre que o valor de tende a 0 quando tende a ao longo de qualquer reta , ou ao longo de qualquer parábola
Ver solução completaQuestão 26
Determine o limite, se existir, ou mostre que o limite não existe (Justifique!)
Ver solução completaQuestão 27
Mostre que o limite de tende a 0 quando ao longo de da curva não existe!
Ver solução completaQuestão 28
Determine o limite, se existir, ou mostre que o limite não existe (Justifique!)
Ver solução completaQuestão 29
Determine o limite, se existir, ou mostre que o limite não existe (Justifique!)
Ver solução completaQuestão 30
Mostre que o valor de tende a 0 quando tende a ao longo de qualquer reta , ou ao longo de qualquer parábola
Ver solução completaQuestão 31
Determine o limite, se existir, ou mostre que o limite não existe (Justifique!)
Ver solução completaQuestão 32
Considere a função
Podemos dizer que:
- existe e varia com
- existe e varia com
- Nenhuma das outras afirmativas está correta.
Questão 33
Determine o limite, se existir, ou mostre que o limite não existe (Justifique!)
Ver solução completaQuestão 34
Determine o limite, se existir, ou mostre que o limite não existe (Justifique!)
Ver solução completaQuestão 40
Considere a função:
- Calcule o limite ou mostre que esse limite não existe.
- Calcule o limite ou mostre que esse limite não existe.
- é contínua em ? Justifique.
- é contínua em ? Justifique.
Questão 42
Determine o limite, se existir, ou mostre que o limite não existe (Justifique!)
Ver solução completaQuestão 46
Determine o limite, se existir, ou mostre que o limite não existe (Justifique!)
Ver solução completaQuestão 48
Considere a função
para todo e . O valor do limite é
a) .
b) .
c) .
d) .
e) inexistente.
Ver solução completaQuestão 49
Mostre que o limite de tende a 0 quando ao longo de da curva não existe!
Ver solução completaQuestão 50
Considere a função
Podemos dizer que
existe e varia com .
existe e varia com .
Ver solução completa
Questão 51
Determine o limite, se existir, ou mostre que o limite não existe (Justifique!)
Ver solução completaQuestão 52
(Cap. 14.2 – Ex. 13) Determine o limite, se existir, ou mostre que o limite não existe.
Ver solução completaQuestão 54
Considere a função
para todo e . O valor do limite é
a) .
b) .
c) .
d) .
e) inexistente.
Ver solução completaQuestão 55
Para cada um dos itens a seguir, mostre se o limite existe ou não. Determine o limite caso exista e justifique suas respostas.
Questão 56
Para cada um dos itens a seguir, mostre se o limite existe ou não. Determine o limite caso exista e justifique suas respostas.
Ver solução completaQuestão 57
Para cada um dos itens a seguir, mostre se o limite existe ou não. Determine o limite caso exista e justifique suas respostas.
Ver solução completaQuestão 59
(Cap. 14.2 - Ex. 14) Determine o limite, se existir, ou mostre que o limite não existe.
Ver solução completaQuestão 61
Considere a função
- Determine o domínio de
- Encontre uma equação para as curvas de nível e de . Esboce tais curvas no sistema cartesiano.
- Existe ? Justifique sua resposta.
Questão 62
Seja
a) Esboce as curvas de nível de nos níveis e .
b) Existe ? Justifique.
Ver solução completaQuestão 63
Considere a função e seja a curva de nível de que passa pelo ponto .
- Represente geometricamente o domínio de e Faça um esboço da curva .
- Determine uma parametrização para a curva , isto é, encontre um intervalo e uma função contínua cuja imagem é .
- Decida se existe