Considere a função definida pelo gráfico abaixo,
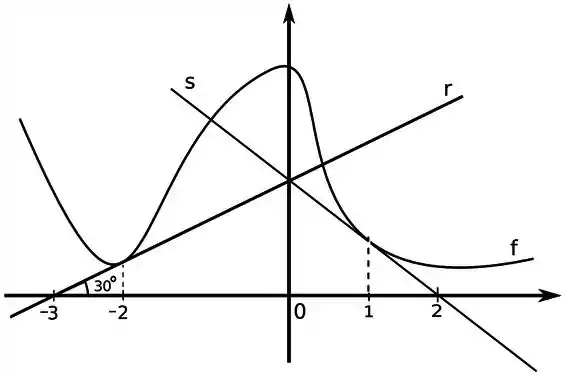
Sabendo que a reta é tangente ao gráfico da em e a reta tangente ao gráfico da em
- Determine a equação da reta
- Determine e
- Determine a equação da reta
- Determine e
Passo 1
Pelo gráfico conseguimos saber a inclinação da reta tangente, isso porque a inclinação da reta vai ser a tangente daquele ângulo que ele colocou ali
Temos um ponto da reta, que é a equação da reta que passa por esse ponto vai ser
Multiplicando cruzado
Passo 2
A reta tangente que passa por vai ser
Multiplicando cruzado vamos ter
Comparando essa reta com a equação que achamos no item vamos ter
Com isso já sabemos a derivada, que vai ser
Substituindo na segunda equação que achamos vamos ter
Passo 3
Para achar essa reta é um pouco mais complicado, não temos a sua inclinação, mas temos um ponto dela que é , outro ponto dela seria mas não sabemos , repara que temos um terceiro ponto que podemos achar, que é o ponto onde a reta corta o eixo , que por acaso é o mesmo que a reta corta o eixo , vamos achar esse ponto pela equação da reta
Devemos fazer
Então aquele ponto que falei é
A equação da reta vai ser
Multiplicando cruzado
Passo 4
A reta tangente que passa por vai ser
Multiplicando cruzado vamos ter
Comparando essa reta com a equação que achamos no item vamos ter
Com isso já sabemos a derivada, que vai ser
Substituindo na segunda equação que achamos vamos ter