USP, Sem Campus, Álgebra Linear 2, Psub - 2017, Questão 5
Considere o espaço vetorial munido do seu produto interno usual e seja o operador linear tal que
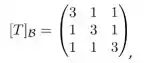
em que denota a base
de. Assinale a alternativa correta:
(a) é diagonalizável e não é simétrico;
(b) não é diagonalizável;
(c) é simétrico;
(d) existe uma base ortonormal C de tal que a matriz é diagonal;
(e) é diagonalizável e não é invertível.
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é descobrir qual das afirmações são verdadeiras. Bora resolver essa questão!!!
Bem, temos que
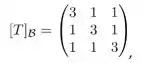
Mas queremos saber coisas sobre , vamos representar na base canônica. Isto é queremos encontrar . Temos que
Sejam e e os vetores da base lacônica de Então, pela definição de , temos:
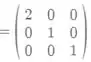
E temos que:
Passo 2
Agora, vamos fazer as contas.
Daqui, já podemos ver que não é simétrica. Mas será que é diagonalizável?
Vamos começar calculando o polinômio característico de . Por definição, ele é:
Temos um autovalor com multiplicidade , então, para ser diagonalizável, os autovetores associados ao autovalor precisam formar um espaço de dimensão .
Passo 3
Calculando os autovetores associados ao autovalor temos:
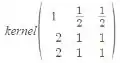
Olhando para as colunas dessa matriz, vemos que temos linhas , logo a dimensão do núcleo será , ou seja, a dimensão do autoespaço associado ao autovalor é . Dessa forma, podemos concluir que é diagonalizável.
Logo a alternativa correta é a letra
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊