USP, Álgebra Linear 2, 2019.1, P2, Q8
Seja um operador linear tal que:
Em que
E can denota a base canônica de . Temos que é igual a:
Passo 1
Faaaala, galerinha do mal! Os elementos descritos acima referem-se à diagonalização de matrizes. Para a qual:
Onde possui suas colunas formadas por uma base de autovetores de e a matriz diagonal possui os autovetores de por elementos da diagonal principal.
Daí, extraímos as relações
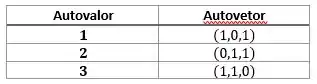
Agora, basta escrever o vetor desejado nessa base de autovetores.
Passo 2
Veja que:
Partindo para a notação matricial do sistema:
Passo 3
Dessa forma, a linearidade garante:
Resposta
Exercícios de Livros Relacionados
Seja A =4 0 1 2 3 2 1 0 4 Será A diagonalizável? Justifique sua conclusão.
Dizemos que uma matriz A n × n é diagonalizável se seu operador associado T A : R n → R n for diagonalizável, ou seja, A é diagonalizável se, e somente se A admitir n autovetores L I . Baseado nisto,
Dizemos que uma matriz A n × n é diagonalizável se seu operador associado T A : R n → R n for diagonalizável, ou seja, A é diagonalizável se, e somente se A admitir n autovetores L I . Baseado nisto,
Dizemos que uma matriz A n × n é diagonalizável se seu operador associado T A : R n → R n for diagonalizável, ou seja, A é diagonalizável se, e somente se A admitir n autovetores L I . Baseado nisto,
Dada a matriz: A = 2 1 0 0 0 2 0 0 0 0 2 0 0 0 0 3 A é diagonalizável?Encontre seu polinômio minimal.