Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Diagonalização

Ver Teoria
Exercício 37123456789101112131415161718192021222324252627282930313233343536383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091

Enunciado

USP, Sem Campus, Álgebra Linear 2, P2 - 2017, Questão 15

Seja T : R 3 → R 3 um operador linear tal que

K e r ( T ) = [ 1,0 , - 1 ] ; K e r ( T - 2 I ) = [ 1,0 , 1 ] ; K e r ( T - I ) = [ 0,1 , 1 ]

Seja A a matriz que representa T na base canônica de R 3 . E seja D a matriz

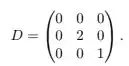
Considere as seguintes matrizes inversíveis

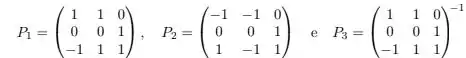
Dentre P 1 ,   P 2   e   P 3 , as matrizes P tais que A   =   P   D P - 1 são:

  1. P 2   e   P 3
  2. P 2
  3. P 1
  4. P 1   e   P 2
  5. P 3

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é descobrir qual das matrizes P 1 , P 2   e   P 3 satisfazem A   =   P   D P - 1

Como vamos fazer isso? Vamos usar o processo de diagonalização de matrizes.

Passo 2

Vamos começar calculando os autovalores e autovetores de T . Por definição, os autovetores v e os autovalores a são tais que

K e r ( T - a I ) = v

Como

K e r ( T ) = [ 1,0 , - 1 ] ; K e r ( T - 2 I ) = [ 1,0 , 1 ] ; K e r ( T - I ) = [ 0,1 , 1 ]

Temos que os autovalores são 0,2   e   1 . E os autovetores são [ 1,0 , - 1 ] ; [ 1,0 , 1 ] ; [ 0,1 , 1 ]

Logo, podemos usar a diagonalização de matrizes. Que diz que T é diagonalizável se pode ser escrito na forma   P   D P - 1 . Onde D é uma matriz diagonal formada pelos autovalores de T e P a matriz onde as colunas são os autovetores de T , onde os autovetores precisam estar na mesma ordem dos seus respectivos autovalores em D .

Passo 3

Mas olha que legal, o enunciado já nos disse quem é D , e pela definição de P , vemos que P 1 é a matriz formada pelos autovetores de T

Logo T na base canônica pode ser representado como

A = P 1 D ( P 1 ) - 1

Mas ainda não terminamos. Consegue ver o porquê?

Note que

P 2 = - P 1

Logo,

P 2 D ( P 2 ) - 1 = - P 1 D ( - P 1 ) - 1

= P 1 D ( P 1 ) - 1

Que já vimos que é A . Dessa forma, concluímos que P 1   e   P 2 são as matrizes P tais que A   =   P   D P - 1

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

d)

Exercícios de Livros Relacionados

Seja A =4 0 1 2 3 2 1 0 4 Será A diagonalizável? Justifique sua conclusão.
Dizemos que uma matriz A n × n é diagonalizável se seu operador associado T A : R n → R n for diagonalizável, ou seja, A é diagonalizável se, e somente se A admitir n autovetores L I . Baseado nisto,
Dizemos que uma matriz A n × n é diagonalizável se seu operador associado T A : R n → R n for diagonalizável, ou seja, A é diagonalizável se, e somente se A admitir n autovetores L I . Baseado nisto,
Dizemos que uma matriz A n × n é diagonalizável se seu operador associado T A : R n → R n for diagonalizável, ou seja, A é diagonalizável se, e somente se A admitir n autovetores L I . Baseado nisto,
Dada a matriz: A = 2 1 0 0 0 2 0 0 0 0 2 0 0 0 0 3 A é diagonalizável?Encontre seu polinômio minimal.