Seja uma transformação linear dada por:
(a) Calcular os autovalores de T.
(b) Calcular os autovetores de T.
(c) T é diagonalizável? Justificar. Em caso afirmativo, encontre uma base na qual a matriz de T é uma matriz diagonal D. E exiba D.
Passo 1
Antes de começar a resolver a questão, vamos escrever T como uma matriz.
Vai ficar assim:
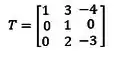
Passo 2
(a) Para calcular os autovalores de T, precisamos encontrar as raízes do polinômio característico, que é:
Vamos começar então encontrando a matriz :
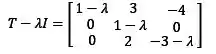
Calculando o determinante e igualando a zero:
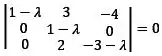
Então achamos os autovalores:
Passo 3
(b) Para encontrar os autovetores, usamos a definição de autovetor para cada autovalor que achamos na letra (a).
Vamos começar aplicando a definição para o autovalor .
Se é autovetor associado ao autovalor , então:
Ficamos então com o sistema:
Da primeira equação, tiramos que:
Substituindo na terceira:
Logo:
E a solução do sistema vai ser dada por:
Portanto, o autoespaço é:
Agora vamos fazer a mesma coisa para o autovalor .
Se é autovetor associado ao autovalor , então:
Vamos ficar com o sistema:
Da segunda equação, tiramos que:
Substituindo na primeira:
Então, a solução vai ser dada por vetores da forma:
E o autoespaço é:
Passo 4
(c) Lembra que uma matriz é diagonalizável somente se a soma das dimensões dos autoespaços associados a cada autovetor de A é n??
A nossa matriz é uma matriz , e já calculamos os autoespaços associados a cada autovalor no item (b).
Nós vimos que:
Então:
que é menor do que 3.
Logo, T não é diagonalizável.
Resposta
(a) e
(b) e
(c) T não é diagonalizável.