Exercícios Resolvidos de Teorema de Stokes

Exercício 34 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

Enunciado

Considere o campo de vetores Use o Teorema de Stokes para calcular

onde C é a fronteira da parte do paraboloide que está no primeiuro octante e orientada no sentido anti-horário quando o bordo é visto de cima.

Passo 1

Vamos lá, antes de mais nada, para podermos ver a possibilidade de aplicarmos o teorema de stoeks, temos que conferir as condições. A primeira dela é termos uma curva fechada. Nesse caso, a curva é a fronteira desse paraboloide no primeiro octante. Então até ai tudo certo.

O campo não pode ter nenhuma singularidade:

Está tudo bem com esse campo.

Por último, mas não menos importante, vamos ter que tomar cuidado com a orientação, pra mantê-la positiva.

Bom, com isso podemos então aplicar o teorema.

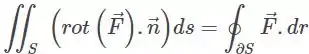
Passo 2

Vamos começar calculando o rotacional:

Passo 3

Vamos agora para nossa parametrização:

A superfície é:

Logo, com uma parametrização explícita ficamos com:

Nosso vetor normal então fica:

Para isso vamos fazer:

Podemos com isso então partir para matriz:

Passo 4

Montando agora então nossa integral:

Resposta

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k

Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d

Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi

Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .

Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê