22) Verifique o teorema de Stokes, calculando as duas integrais do enunciado para...
b) , o hemisfério , orientada com normal unitária exterior a .
Passo 1
O enunciado do Teorema de Stokes nos dá a seguinte relação...
É basicamente essa igualde mara entre as integrais de linha e de superfície! O problema quer que calculemos as duas para verificar Stokes.
Poxa! #exercícioimenso #socorrorespondeaí!
Lógico! Bora lá que eu te ajudo 😉
Passo 2
AHHH! Mas Stokes não é só isso! Se não taria muito bom, ne? Para aplicar essa igualdade, antes devemos averiguar as condições desse Teorema, que nos pede basicamente três coisas:
1º - Uma curva fechada delimitando a superfície .
2º - Sem singularidades na função Vetorial.
3º - Superfície orientada positivamente.
Vamos passar por cada um deles e verificar se satisfazem ou não 😊!
Passo 3
A superfície que delimita é, no nosso caso, um hemisfério norte da esfera de raio ...
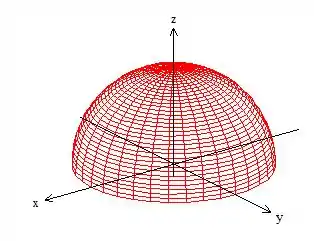
Veja que a curva que delimita a superfície é essa borda em azul escuro que vamos nomeá-la de curva .
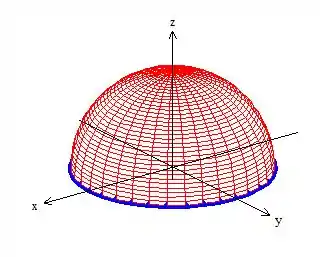
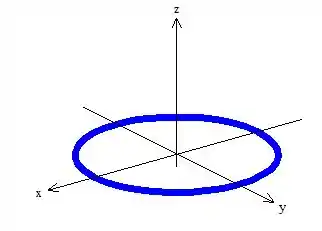
Então pelo esboço, sim! Temos uma curva fechada e que delimita uma superfície fechada entre ela, no caso que é a esfera (mas também delimita um pedacinho de disco em percebeu? 😊)
Passo 4
2º - Sem singularidades na função Vetorial.
Ora, sim! Basta ver o campo
Para você perceber que o campo não tem nenhum bug ou singularidade, como uma divisão por em algum ponto ou algo assim.
Passo 5
3º - Superfície orientada positivamente.
Aqui o que temos que fazer é garantir que o conjunto curva-superfície esteja orientadas positivamente, ou seja, se o problema nos disse que é o vetor que está saindo de (esfera)
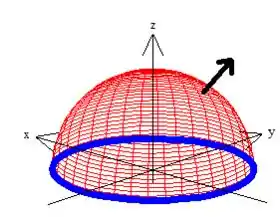
Então pela regra da mão direita a curva deve estar girando no sentido anti-horário quando vista de cima:
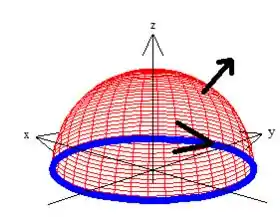
Agora elas estão sim orientadas positivamente, saca?
Passo 6
Bem, nas condições do Teorema podemos sim aplicar a igualdade de boa:
Para calcular a integral de linha, façamos:
1º - Parametrizar a curva ...
2º - Encontrar o termo ...
3º - Trocar os termos de pela parametrização.
Passo 7
Primeiro em relação a parametrização da curva : pametrizando com a parametrização polar...
Onde não é parâmetro, afinal como é uma curva só tem um parâmetro (). é o raio da circunferência que no caso ... Logo a parametrização final dessa borda é...
Onde tem que dar uma volta completa ao redor do ...
Observa que essa forma de parametrizar o gira no sentido que a gente quer, ou seja, anti-horário quando vista de cima. E isso acontece sempre nessa parametrização 😉!
Passo 8
A curva já está parametrizada positivamente. Para o termo , basta derivar em relação a
...
Passo 9
Por fim, antes de voltar para a integral de linha... O campo tem que ser transformado nas novas coordenadas (basta observar a parametrização) ...
Voltando para a integral de linha...
Calculando o produto escalar:
Lembrando que
Passo 10
Bem, como averiguamos as condições do Teorema de Stokes e todas funcionaram, então é porque com certeza a integral de superfície do rotacional deve dar
Massss... Como o problema nos pediu para confirmar... Vamos confirmar:
Calculando o rotacional
Então...
Precisamos agora:
1º - Parametrizar a superfície
2º - Encontrar o termo
Passo 11
Para parametrizar, podemos fazer isso utilizando parametrização explícita já que a superfície está bem escrita explicitamente em relação em ...
Logo...
Onde e variam na circunferência de raio ... (como se tivéssemos olhando para a calota de cima pra baixo) ...
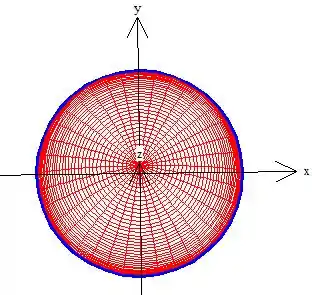
Passo 12
Para determinar o termo ...
Só que esse vetor é fácil de ser determinado, pois parametrizamos como gráfico de função...
Logo...
Passo 13
Jogando esses resultados na integral de superfície...
Calculando esse produto interno...
Usando as coordenadas polares, onde...
E uma equação muuuuito interessante é a equação da circunferência...
Onde varia de...
E o ...
Montando a integral...
Separando as integrais em duas...
Calculando a primeira integral em ...
Calculando a outra integral...
Logo...
Como já esperávamos 😉