Exercícios Resolvidos de Teorema de Stokes

Ver Teoria

Exercício 6 1 2 3 4 5 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

Enunciado

Usando o teorema de Stokes, calcule o trabalho realizado pelo campo de forças

quando uma partícula se move sob sua influência ao longo da curva de interseção das superfícies e , orientada no sentido anti-horário quando vista de cima.

Passo 1

Galerinha, a gente começa relembrando um pouco lá da física, onde trabalho é força vezes o deslocamento. Então, neste caso, podemos escrever o trabalho dessa forma aqui:

Para resolver essa integral vamos utilizar o Teorema de Stokes. Então teremos essa igualdade aqui:

Onde a curva é o bordo da superfície orientada positivamente.

Passo 2

A gente vai começar, esboçando essas superfícies para entender melhor o problema.

O enunciado forneceu a equação de duas superfícies.

A primeira é a equação da esfera, cujo raio é :

Já a segunda equação é um plano:

Esboçando as duas curvas, temos:

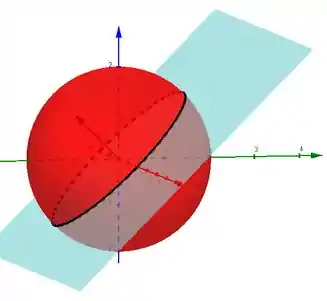
A interseção da esfera com o plano é uma elipse. Para achar essa elipse, basta substituir a equação do plano () na equação da esfera:

Dividindo tudo por , para se encaixar na equação geral da elipse:

Beleza?? Essa é a nossa elipse que será a interseção entre o plano e a esfera!

O enunciado também diz que ela está orientada no sentido anti-horário vista de cima. Deste modo, pela regra da mão direita, podemos ver que o vetor normal à superfície deve estar apontando para cima para aplicarmos o teorema de Stokes.

Passo 3

Agora vamos partir para integral!

Precisamos do rotacional do campo ! O rotacional é dado por:

Como nosso campo é

Temos que,

Calculando, ficamos com

Passo 4

Repara que na nossa integral temos o rotacional é multiplicado pelo vetor normal!

Então, precisamos do vetor normal à superfície .

Observando o esboço da superfície, vemos que a elipse que queremos orientar está contida no plano . Se não ficou claro, é só reparar que o o vetor normal sai do centro e avança para valores de negativos e positivos. Aahh, repara que ele não tem componente em .

Escrevendo na forma vetorial, temos

Ele é um vetor normal à superfície sobre a qual estamos integrando com a orientação que queremos.

Passo 5

Já temos todos os elementos, vamos para integral! Ela fica assim:

Então, temos que achar a área da superfície formada pela interseção do plano com a esfera. Como já vimos, nossa superfície é a elipse:

Como a equação geral da elipse é:

Temos, aqui, e .

Então, basta a gente calcular a área dessa elipse, que é dada por :

Dessa forma, podemos substituir em :

Logo, esse é o valor do trabalho pedido na questão! 😊

Resposta

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k

Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d

Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi

Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .

Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê