Sejam e superfícies regulares com equações implícitas e , respectivamente, e seja a curva obtida na intersecção de e , orientada de modo que suas projeções no plano é percorrida no sentido anti-horário.
(a) Esboce as curvas obtidas na intersecção de e com o plano
(b) Mostre que a curva está contida num plano e encontre a equação implícita para o plano que a contém.
(c) Mostre que a curva está contida num clilíndro cujo eixo de rotação é paralelo ao eixo e encontre a equação implícita.
(d) Usando o teorema de Stokes, descreva uma superfície apropriada que tenha a curva como fronteira e calcule o trabalho do campo
Passo 1
Letra a)
Para facilitar a nossa vida vamos considerar já a intersecção com o plano , dessa forma nossas duas equações serão:
Dessa forma facilita muito a nossa vida porque agora só precisamos desenhar em um plano essas nossas duas equações de parábolas
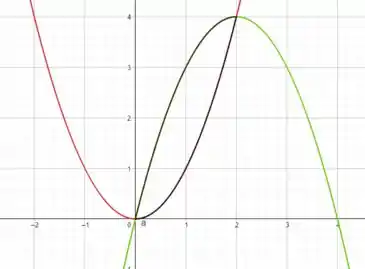
Onde as curvas que a gente quer são essas que estão em preto.
Para finalizar e deixar mais completo igualamos as duas equações para marcamos os ponto de intersecção.
Rearranjando essa equação teremos então:
As raízes dessa equação nos dirá que nossos pontos terão como coordenadas em : e
Para descobrir o valor em é só substituir em uma das equações que tínhamos e agora nossos pontos serão:
e
Passo 2
Letra b)
Tendo as equações das superfícies:
e
Organizando a segunda equação para termos de um lado só:
Substituindo na primeira equação vamos ter:
Que é a equação implícita do plano que contém a curva
Para ter uma visualização do plano.
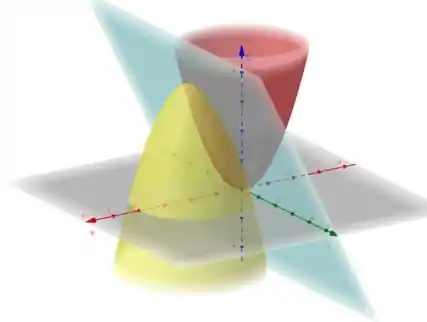
Passo 3
Letra c)
Tendo as equações das superfícies:
e
Substituindo em uma equação da outra vamos ter:
Organizando a equação:
De primeiro momento não parece ser a quação de um cilindro, mas para ficar mais claro, vamos somar 1 dos dois lados para podermos completar o produto notável de
Assim fica mais claro que temos um cilindro de raio e deslocado de uma unidade em com relação à origem.
Essa é portanto a equação do cliíndro que contém a curva . Note que como temos a variável omitida, significa que o cilindro é projetado ao logo desse eixo.
Para ter uma visualização melhor de como seria o cilindro.
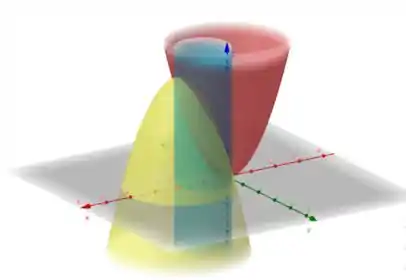
Passo 4
Letra d)
Para utilizar o teoremas de Stokes precisamos que a curva seja fechada e que ela seja o bordo de uma superfície.
O teorema de stokes pode ser calculado fazendo:
O que queremos é o trabalho do campo , que é exatamente essa integral de linha do lado esquerdo da equação.
Vamos começar calculando o rotacional do campo. Esse rotacional é calculado pela fórmula:
Calculando cada derivada parcial separadamente:
O rotacional será portanto:
Passo 5
A melhor superfície para esse caso é a superfície no interior da curva , que chamaremos de .
Ela pode ser encontrada igualando as equações das superfícies e :
(1)
(2)
Assim vamos ter igualando :
Aqui temos a equação de um cilindro
Precisamos ainda igualar a parte de :
Substituindo isso em (1):
O que temos aqui é a equação de um plano.
Portanto podemos definir a superfície quem a gente quer como:
Onde:
Passo 6
Encontrado a normal à nossa superfície
Como a normal deve apontar para fora uma vez que já foi definido uma orientação anti-horária para a projeção da curva no plano , manteremos essa normal.
Passo 7
Vamos agora aplicar a fórmula:
Onde é dado por
Passo 8
Fazendo agora a mudança polar:
Os limites agora passam a ser:
Jogando isso tudo na nossa integral:
Resposta
a) 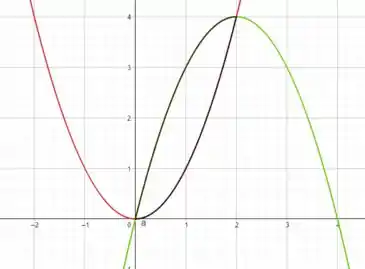
b)
c)
d)