Sejam uma região sólida simples com fronteira e um campo vetorial de classe tal que é uma região aberta contendo . Mostre que
Isto é, o fluxo do rotacional de através de é zero.
Passo 1
Beleza, vamos lá. Sabemos que é o rotacional do campo vetorial , então podemos escrever:
Que é o mesmo que:
Show? Onde é o campo de vetores normais à superfície .
Passo 2
Show, pelo Teorema de Stokes, temos que:
Logo,
Ou seja, a integral de superfície que o problema quer pode ser substituída por uma integral de linha na fronteira de .
Agora vamos pensar um pouquinho. Temos , que é um sólido e , que é a superfície fronteira de . A fronteira de , seria uma curva. Porém, se é um sólido, então é uma superfície fechada, certo? Logo, ela não tem fronteira alguma. Então esse fluxo seria nulo, mas isso é só especulação, precisamos provar!
Passo 3
Bom, já que não temos uma fronteira, vamos começar criando uma, ok? Para podermos visualizar, vamos imaginar que esse sólido seja uma esfera, com vetores normais apontando para fora dela:
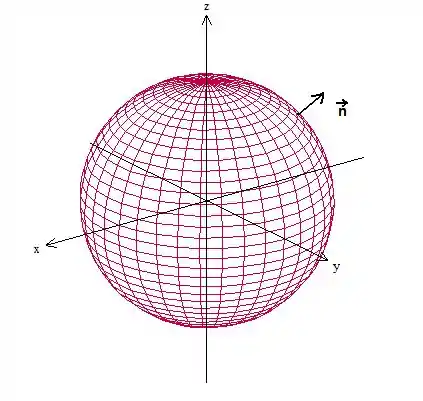
Gente, o sólido não é uma esfera, é um sólido qualquer! Estamos só imaginando que seja para facilitar o entendimen.te
Beleza, agora vamos dividir esse sólido em duas partes, :
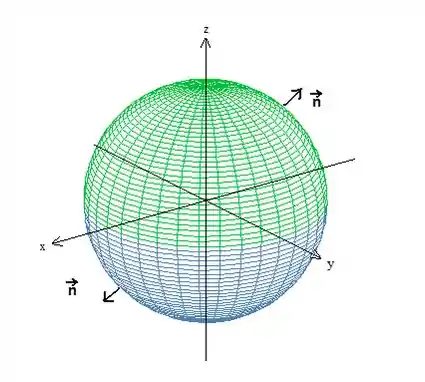
As duas partes mantém a mesma orientação. Temos, então, duas superfícies tais que . Logo:
Passo 4
Até aí tudo ok? Beleza, agora vamos tratar das duas integrais separadamente. Pensando na casca de cima, , se sua orientação é essa, a borda de é orientada da seguinte forma:
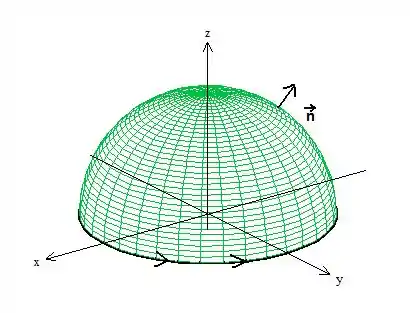
Pela regra da mão direita, lembra? Com tais orientações, podemos dizer, pelo Teorema de Stokes, que:
Para , temos o contrário:
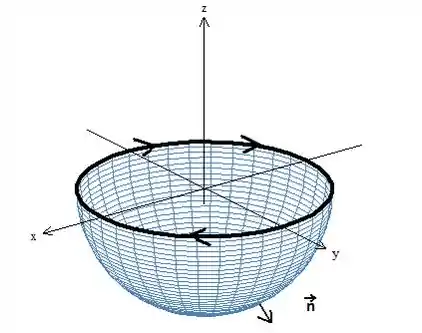
Com essas orientações, podemos dizer que
Passo 5
Show, agora, como
Temos
Ótimo e agora??
Agora pensa um pouco, as fronteira de e tem o mesmo formato, são exatamente a mesma curva (afinal, as duas cascas formam um sólido), porém com orientação contrárias.
Se você reparar nos desenhos, tem orientação anti-horária e orientação horária (considerando o sólido orientado com normais apontando para fora). Portanto, podemos dizer que:
Ou seja, trocando o sentido de , as integrais são as mesmas. Isso é o mesmo que:
Olha que mágico então
Pronto, provamos que a integral dá zero.
Obs: esse raciocínio funciona para qualquer sólido, sendo uma esfera ou não! Sendo simétrico ou não! A base da questão é perceber que, sendo um superfície fechada, ela não possui fronteira e que, dividindo o sólido em duas partes quaisquer, as fronteiras das duas partes possuem o mesmo formato, porém, orientação oposta. Logo, as integrais de linha se anulam.
Resposta
Ei, a resposta está no passo a passo :)