28) Calcule a circulação do campo ao redor da curva fronteira do triângulo recortado do plano pelo primeiro octante, no sentido horário quando vista da origem.
Passo 1
Quando o problema nos pede para calcular a circulação ao redor de uma curva, o que ele no fundo está querendo de nós é que calculemos uma integral de linha desse campo em cima da curva :
Tem dois meios basicamente que podemos resolver isso aí:
1º - Resolver pelo método diretão.
2º - Resolver pelo teorema de Stokes.
Veja bem, a curva que estamos trabalhando é a intersecção do plano no primeiro octante, veja:
Pow, o campo não é tão feio, então você poderia pensar em usar a primeira opção, o método direto. A má notícia quanto a essa escolha é que a curva por ser composta daria muuuuuuito trabalho para calcular essas integrais! 😐
E é por isso que a melhor saída é a segunda opção! Mas se você quer uma prova mais visual podemos calcular o Rotacional de ...
Como
Então...
Pow, com um rotacional desse é a prova visual de que Stokes pode ser bem mais elegante, saca?
Passo 2
Tão tá bom sabemos que Stokes pode resolver o problema, mas o que ele fala mesmo? Bem basicamente ele iguala a integral de linha com uma de superfície dessa forma aqui:
Assim, ao invés de termos que calcular uma integral de linha, podemos calcular uma integral de superfície 😉!
Porém Stokes não é só isso! Se não taria muito bom, ne? Para aplicar a igualdade entre as integrais antes devemos averiguar as condições desse Teorema, que nos pede basicamente três coisas:
1º - Uma curva fechada delimitando uma superfície .
2º - Sem singularidades na função Vetorial.
3º - Superfície orientada positivamente.
Vamos passar por cada um deles e verificar se satisfazem ou não 😊!
Passo 3
Já desenhamos a nossa curva e ela é fechada. Veja ala aqui novamente:
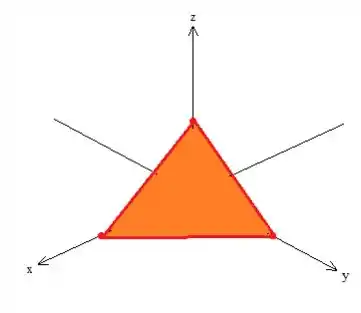
Essa curva delimita várias superfícies, mas uma mais simples que a você deve ter notado é a que está no próprio plano (o triângulo).
Bem, a essa superfície daremos um nome hiper carinhoso de (superfície 😊)
Passo 4
A outra condição é:
2º - Sem singularidades na função Vetorial.
Ora, sim! Basta ver o campo
Para você perceber que o campo não tem nenhum bug ou singularidade, como uma divisão por em algum ponto ou algo assim.
Passo 5
3º - Superfície orientada positivamente.
Aqui o que temos que fazer é garantir que o conjunto curva-superfície esteja orientadas positivamente, ou seja, como a curva no gira no sentido horário quando vista de origem... Imagine que estamos na origem. Pra vermos a curva girando no sentido anti-horário então...
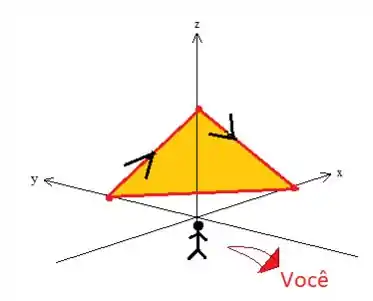
Vendo de outro ângulo...
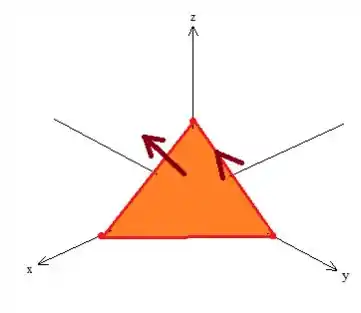
Ela está girando no sentido anti-horário quando vista de cima então, viu só? Pela regra da mão direita temos que ter um vetor normal pra cima na superfície.
Agora elas estão sim orientadas positivamente, saca?
Passo 6
Com as condições averiguadas e sendo satisfeitas, podemos aplicar a igualdade numa nice:
Para calcular a integral de superfície, precisamos:
1º - Parametrizar a superfície .
2º - Encontrar o termo .
Bora?
Passo 7
Para parametrizar a superfície saca só: estamos em cima de um plano...
Então podemos parametrizar de forma explícita, pois o é um cara livre (parâmetro) e depende de que também é um cara livre...
Agora esses parâmetros e estão variando dentro da projeção no plano ...
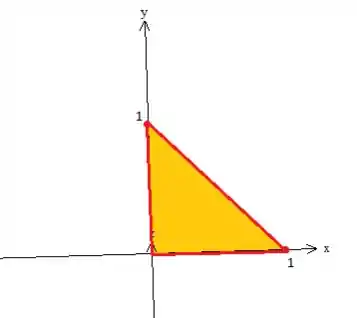
Veja que esse triângulo tem aquela reta vermelha escura ali sendo a reta de quando o plano encontra o ... Portanto a equação dessa reta é...
Com isso conseguimos descrever esse triângulo projeção como do tipo , onde varia de até ...
Enquanto o vai de até a retinha vermelha que acabamos de descobrir quem é...
Passo 8
Para o termo ...
Onde o é fácil de se obter pelo macete de parametrização por gráfico de função ...
O mais legal é que esse vetor está nas condições que colocamos para o vetor normal... Apontado pra cima 😊
Então...
Passo 9
Como , o rotacional é...
Jogando esses dados então na integral de superfície...
Como já descrevemos
Calculando a integral...
Então, pelo Teorema de Stokes, o rotacional do campo próximo a curva é...