Use o Teorema de Stokes para calcular
onde e é o femisfério com orientação ascendente.
Passo 1
Beleza então, questão diretona aí pra gente. Vamos lembrar o que é esse Teorema de Stokes?
Bom, nele nós trocamos a integral de Superfície por uma integral de linha, certo?
Vamos começar então calculando o rotacional do nosso campo, tranquilo?
Passo 2
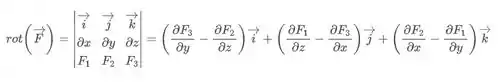
Lembrando que nosso campo é
Bora lá então,
Caraca, melhor que isso é impossível. Temos um campo conservativo!! A integral de linha de um campo conservativo ao longo de QUALQUER curva fechada em seu domínio é nula!
Logo, nossa resposta é zero