Usando o Teorema de Stokes, calcular a seguinte integral de linha:
em que é a superfície orientável com fronteira orientada positivamente, definida pela parametrização.
sendo o triângulo de vértices .
Passo 1
Pelo Teorema de Stokes...
Mas sim, antes de aplicarmos essa igualdade do teorema de Stokes, devemos analisar as condições do Teorema:
1º - Uma superfície fechada delimitada pela borda .
2º - Orientadas positivamente.
3º - E um campo sem singularidades.
Vamos averiguar cada uma dessas condições e depois aplicar a igualdade! ;)
Passo 2
Bem, começando pela primeira exigência, o problema já nos disse que a superfície é uma superfície fechada ao falar que ela tem uma borda e sua borda é a curva fechada .
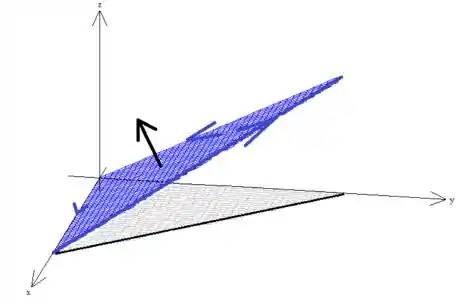
Mesmo já sabendo que essa condição está sendo satisfeita, essa superfície parece ser fácil de desenhar:
Ela está parametrizada da seguinte forma:
Nessa parametrização, observamos que é do tipo explícita, onde...
representa um plano paralelo ao eixo , dessa forma...
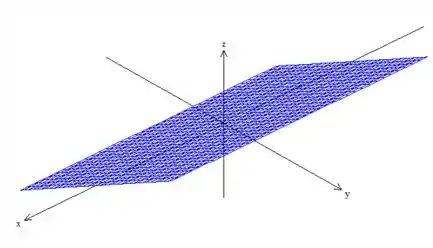
Então a superfície é esse plano aí. Mas é claro, existe uma delimitação. Vamos ver isso com mais calma!
Passo 3
A delimitação é que... . Logo, .
Como é um triângulo de vértices... :
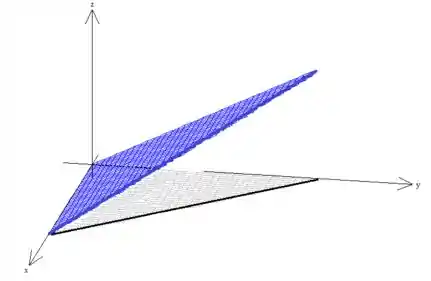
Esse triângulo azul é a restrição da superfície ... Sacou?
Passo 4
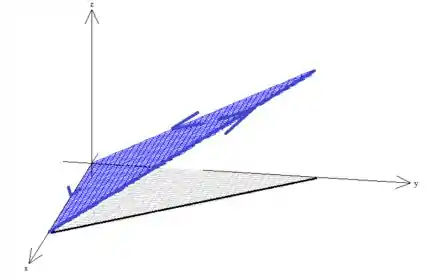
Quanto à segunda condição do teorema, sobre orientada positivamente, esse também está sendo satisfeito por natureza, afinal o próprio enunciado nos disse isso.
Isso só pode significar que a borda da superfície gira no sentido anti-horário quando vista de cima:
Pela regra da mão direita, sabemos então a direção do vetor norma à superfície que torna essa condição verdadeira:
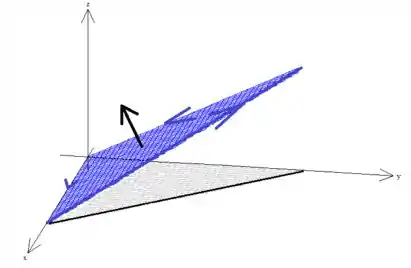
Agora sim, garantimos que a borda/superfície, estejam orientadas positivamente ;)
Passo 5
A última condição do teorema nos pede uma função sem singularidades...
Repare que em nenhum ponto esse função dá problema, como uma divisão por ou algo do tipo!
Passo 6
As três condições analisadas e satisfeitas, podemos enfim aplicar a igualdade:
Então, repare que estamos trocando o problema de calcular a integral de linha por outro de calcular a integral de superfície. Então vejamos quem é esse rotacional...
Como...
Passo 7
Para resolver essa integral de superfície precisamos:
1º - Parametrizar a superfície.
2º - Obter o termo .
3º - Obter o rotacional em termos da parametrização.
Então vem comigo!
Passo 8
Para a nossa alegria, a superfície já está parametrizada:
Sabemos que e variam no triângulo cinza:
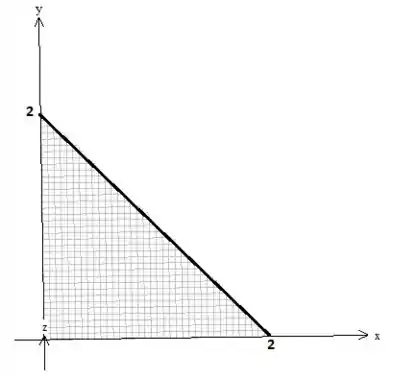
Então precisamos descrever esse triângulo onde podemos fazer isso, considerando a região do tipo , onde varia entre um intervalo numérico e entre funções:
Quanto à variação de
A equação dessa reta na diagonal é , pois só assim quando , e quando , sacou?
Então...
Passo 9
Para obter o termo :
E
Como...
Lembrando que o produto vetorial é um determinante...
Logo, o vetor normal é...
Como esse vetor normal está pra cima ele satisfaz a condição de orientada positivamente como vimos, logo é esse mesmo que queremos...
Passo 10
Por último antes de voltar para a integral de superfície, vamos trocar a função ...
e ...
Passo 11
Voltando à integral de superfície que queremos matar...
Substituindo tudo...
Calculando a integral dupla...
Pela igualdade de Stokes, temos então que...
Resposta
Exercícios de Livros Relacionados
Ver Mais
Ver Mais
Ver Mais
Ver Mais
Ver Mais