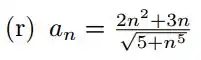
Passo 1
Tá meio complicado de analisar essa série nesse formato. Vamos manipular ela um cado.
Parece que ficou bem mais feio, mas esse formato vai ajudar a gente a determinar a divergência utilizando o teste da comparação com a serie harmônica.
Passo 2
O termo geral da nossa série é bem estranho, mas podemos afirmar que.
Dessa forma, só precisamos determinar a convergência da série com esse termo simplificado e fácil de trabalhar.
Sem muito trabalho conseguimos notar que
Logo, pelo teste da comparação, a nossa série irá divergir.
Resposta
A série diverge.
Exercícios de Livros Relacionados
Suponha que ∑ a n e ∑ b n sejam séries com termos positivos e que ∑ b n seja divergente.(a) Se a nb n para todo n , o que você pode dizer de ∑ a n ? Por quê?(b)Se a nb n para todo n , o que você pode
Determine se a série converge ou diverge.5. ∑ n = 1 ∞ n + 1 n n
Determine se a série converge ou diverge. ∑ n = 1 ∞ n 3 n 4 - 1
Determine se a série converge ou diverge. ∑ n = 1 ∞ 1 n 2 + n + 1
Determine se a série converge ou diverge.sum_(n = 1)^(oo) (1)/(root(3)((3 n^4 + 1)))