PUCRIO – Física 1 – 2020.1 – P2 – M. Escolha
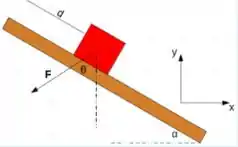
. Um bloco de massa é deslocado para cima, por uma força constante, uma distância ao longo de um plano inclinado. O plano está inclinado de em relação à horizontal, e a força faz um ângulo com a vertical. Determine o trabalho realizado pela força ao longo do deslocamento. Utilize o sistema de coordenadas indicado na figura.
Passo 1
Vem comigo que a gente detona com essa questão!
O enunciado quer o trabalho realizado pela força . O trabalho é dado pela força vezes a distância que essa força foi aplicada.
O bloco dessa situação ele tem um deslocamento tanto no eixo quando no eixo . Assim como a força tem componentes na direção e .
Então nessa situação temos trabalho, tanto na direção , quanto na direção , assim:
Então temos que achar as componentes da força nessas direções e a achar o deslocamento do bloco nessas direções.
Passo 2
Vamos começar com a direção .
O bloco se desloca na direção negativa de e como ele se desloca com um ângulo com o eixo , temos que:
A componente da força nessa direção aponta para o sentido negativo de , e com a força faz um ângulo com a vertical, temos que:
Então temos que o trabalho nessa direção é dada por:
Passo 3
Agora vamos analisar a direção .
O bloco se desloca na direção positiva de e como ele se desloca com um ângulo com a horizontal, temos que:
A componente da força nessa direção aponta para o sentido negativo de , e com a força faz um ângulo com o eixo , temos que:
Então temos que o trabalho nessa direção é dada por:
Passo 4
Juntando tudo temos que o trabalho realizado pela força , é dado por:
E com isso terminamos a questão!