- Defina precisamente partição de um intervalo.
- Defina precisamente soma de Riemann.
Passo 1
Oi, lindezas! Todo mundo pronto para uma questão bem teórica? Se você acha que nem lembra como escrever sem matematiquês, eu vou te ajudar!
Começando com a primeira pergunta:
“Defina precisamente partição de um intervalo”
Em um somatório, como por exemplo:
Temos um intervalo igual a:
E para realizar a soma ponto a ponto, podemos dividir esse somatório em pequenos intervalos, como por exemplo com uma largura igual a , então teremos os pontos dentro desse intervalo:
E o próximo ponto? Se falamos que os intervalos são sempre iguais a , então o próximo ponto é o último ponto mais :
Então chegamos ao próximo ponto:
Podemos aplicar isso a todos os pontos até chegar no último ponto do nosso intervalo:
Logo o nosso intervalo inicial passa a poder ser dividido como um conjunto de pontos:
Essa divisão do intervalo é chamada de partição.
Agora que terminamos a letra “a”, vamos responder a letra “b”!
Passo 2
Bom, na letra “b”, ele nos pede:
“Defina precisamente soma de Riemann”
A soma de Riemann nada mais é do que um método para calcular a área delimitada por uma curva, mas calma que eu não vou parar por aqui.
Que curva é essa? Bom, pensa comigo que se tivermos uma função que possua um gráfico como o da figura a seguir em um intervalo :
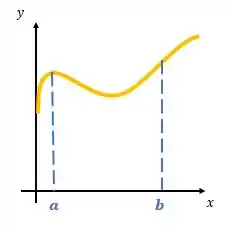
Usando o método da Soma de Riemann, vamos aproximar essa área embaixo dessa curva limitada pelo intervalo com vários retângulos com largura igual as partições que nós falamos no item anterior!
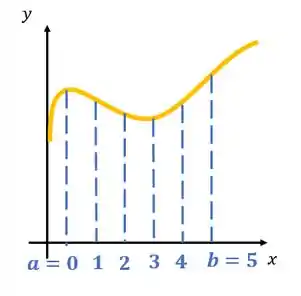
Agora imaginando esses retângulos:
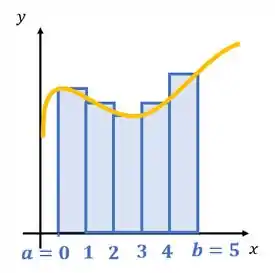
Então, podemos aproximar essa área pela soma de Riemann pela soma dos produtos da base de cada retângulo pela altura de cada retângulo:
E nesse caso a altura é igual a função naquele ponto:
Como temos 5 retângulos, logo a área fica como:
Você concorda que podemos reescrever como:
Pronto! Essa é a soma de Riemann! Nem doeu né? Bora pra próxima!
Resposta
Ei, a resposta está no passo a passo :)