UFJF, Sem Campus, Física 3, AV3 - 2ª CH - 2018.2, Questão 1a
O campo magnético em todos os pontos de uma região cilíndrica de raio é uniforme e direcionada para fora da página, variando com o tempo , onde é uma constante positiva.
Determine a circulação do campo elétrico, , ao longo dos círculos de e percorrido no sentido horário.
Passo 1
Eaew, tudo certinho com você?
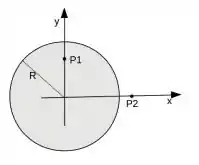
O enunciado nos indica uma região cilíndrica de raio dada por
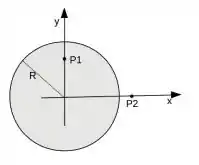
e precisamos calcular a circulação do campo elétrico ao longo dos círculos de raio e . Esse campo elétrico surge devido a variação do fluxo do seguinte campo magnético
que aponta para fora da tela, através da superfície circular delimitada pelo cilindro. Para calcular então a circulação vamos usar a lei de Faraday-Lenz
Sendo assim! Podemos começar calculando o fluxo de nosso campo magnético! Vamos lá!
Passo 2
Temos que é o fluxo do campo magnético, que pode ser calculado usando a seguinte integral de superfície
A última igualdade é verdade, pois o campo é uniforme para todo raio. Desta forma, temos que a nossa integral se reduz à
Se . Vamos resolver cada uma das integrações! Vem comigo!
Passo 3
Usando a regra dos polinômios para integrações, temos que
ou, avaliando os limites de integração, temos que
Usando o resultado em nossa integral de fluxo, temos que
A integral que falta pode ser identificada diretamente como
Portanto, o nosso fluxo é
Vamos usar isso para calcular a nossa circulação! Vem comigo!
Passo 4
Queremos então calcular
Usando a regra do tombo, temos que
E, finalmente, obtemos nossa circulação como
Vamos agora calcular para um , saca só!
Passo 5
A única diferença que temos é mudança dos limites de integração em nossa integral de superfície, como a região pela qual estamos considerando o fluxo acaba, os limites se tornam
As integrais nós já resolvemos nos passos anteriores, obtemos então que
e, a circulação será
da mesma forma que fizemos anteriormente! A primeira alternativa foi isso! Te vejo na próxima! Tchauzinho!
Resposta
Para temos e para temos