Uma carga elétrica pontual encontra-se na origem de um sistema de coordenadas. A uma distância à sua esquerda encontra-se uma carga elétrica pontual , conforme ilustrado na figura 1.
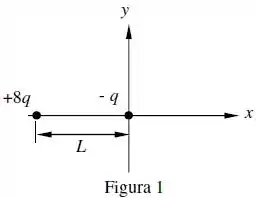
Para tal situação:
Calcule o módulo do campo elétrico gerado em um ponto localizado ao longo do eixo , para .
Determine o ponto sobre o eixo onde o campo elétrico se anula.
Determine o ponto sobre o eixo , onde , no qual o campo elétrico atinge seu valor máximo.
Esboce o gráfico do campo elétrico para pontos ao longo do eixo , para .
Passo 1
Calcule o módulo do campo elétrico gerado em um ponto localizado ao longo do eixo , para .
O campo elétrico gerado por uma carga pontual é dado por:
O campo elétrico resultante em um ponto qualquer é igual à soma vetorial dos campos gerados por cada carga.
Nesse caso, para um ponto qualquer , onde , o campo elétrico será dado por:
Passo 2
Determine o ponto sobre o eixo onde o campo elétrico se anula.
Utilizando a expressão do campo elétrico que encontramos acima, temos:
Agora é só ir organizando esse cara até encontrarmos a expressão de :
Finalmente:
Passo 3
Determine o ponto sobre o eixo , onde , no qual o campo elétrico atinge seu valor máximo.
O campo magnético será máximo quando:
Logo:
Finalmente:
Passo 4
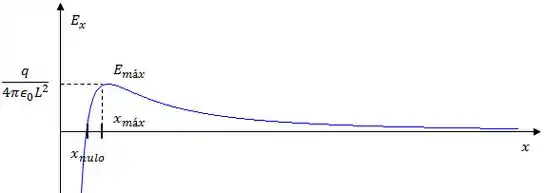
Esboce o gráfico do campo elétrico para pontos ao longo do eixo , para .
Para montar o gráfico, precisamos ficar espertos para alguns detalhes. A equação do campo elétrico é dada por:
O ponto nulo é dado por:
Além disso, podemos testar alguns limites pra ter uma ideia melhor do gráfico:
Dessa forma, o gráfico vai ter mais ou menos essa forma:
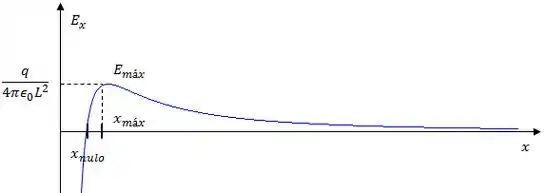
Resposta