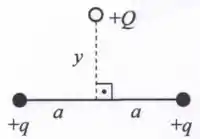
Na figura abaixo, duas cargas pontuais estão separadas por um distância . Uma terceira carga pontual é colocada na linha que passa pelo centro do segmento que conecta as cargas . Sabe-se que a carga está fixa e que se localiza a uma distância , perpendicular ao segmento horizontal de comprimento .
- Calcule o vetor força elétrica total (módulo, direção e sentido) que as cargas exercem na carga .
- Calcule para que valor da distância o módulo da força total na carga é máxima.
- Esboce um gráfico representando como o módulo da força total varia com a distância , onde .
Passo 1
a) A primeira coisa que precisamos nos lembrar aqui é que duas cargas puntiformes quaisquer de mesmo sinal se repelem. Nessa questão, temos três cargas positivas e queremos analisar como é a força resultante que atua na carga .
Para ficar fácil de ver isso, desenhamos, na figura abaixo, as duas forças , devidas às cargas e se afastando delas, que atuam sobre , já que temos apenas forças de repulsão. As forças fazem um ângulo com o eixo e um ângulo de com a direção .
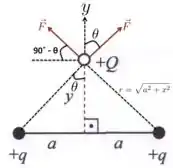
Ainda de olho na figura (sempre ajuda a gente ter uma figura para ver bem como ficam os vetores e as distâncias... ;-) ), vemos que as duas cargas estão à mesma distância de . Além disso, como as cargas têm o mesmo módulo, então as componentes das forças na direção terão mesmo módulo, mesma direção, PORÉM sentidos contrários e, por isso, vão se cancelar. Vamos ter que concentrar agora apenas na direção , que é para onde vai apontar a força resultante , beleza?
Quando somamos as componentes das forças na direção , vamos encontrar . Fazendo isso, encontramos que:
Bom, sabemos também que o módulo é dado por
e que, do triângulo retângulo da figura acima, temos
Isso vai resultar num vetor força resultante dado por:
que mostra que, para , temos .
A gente pode reescrever esse vetor como:
o que facilita para percebermos que para , temos também . Se para e temos , então, como temos uma força que é uma função positiva de . Por isso, ela vai ter um valor máximo, que a gente vai estudar melhor nos próximos itens.
Passo 2
b) Como temos força resultante positiva que é uma função de , para encontrarmos o valor de que maximiza essa função, temos que derivar com relação à variável e igualar o resultado a zero, ou seja,
Desenvolvendo um pouco mais essa derivada, vamos ter que
Resolvendo essa equação, vamos ter que . Como colocamos a carga está acima do eixo , vamos tomar apenas a solução:
que dá o valor máximo para a força resultante .
Passo 3
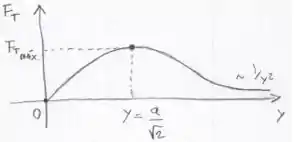
d) Como discutimos no Passo 1, a função força resultante vai ter um valor máximo e esse valor vai acontecer para , como acabamos de calcular. Por isso, o gráfico do comportamento do módulo de será:
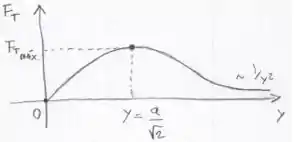
Eu sei! Você provavelmente se emocionou com a qualidade artística do meu gráfico ;)
Resposta
c)