Duas cargas puntiformes são colocadas sobre o eixo , uma no ponto a outra no ponto . Deduza uma expressão para o campo elétrico em qualquer ponto sobre o eixo .
Passo 1
Começar desenhando o problema é sempre uma boa:
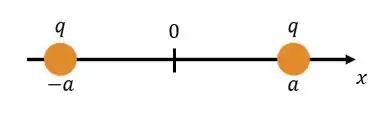
Beleza. À partir do desenho, podemos perceber que temos três regiões críticas:
Não podemos tentar calcular o campo “em cima” de uma das cargas pois a distância dela para si mesma seria zero, o que resultaria numa divisão por zero na fórmula do campo. Beleza? Vamos agora calcular para cada um dos casos.
Passo 2
A expressão para o campo de uma carga puntiforme é a seguinte:
Onde é a distância do ponto que queremos até a carga. Como as duas cargas são positivas vamos ter dois campos divergentes:
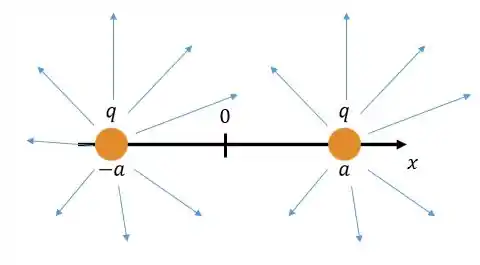
Mas a única linha de campo que nos interessa agora é a que está em cima do eixo :
- Para :
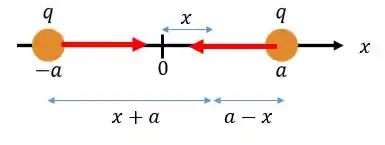
A contribuição da carga em é positiva (aponta para o sentido positivo de ), já a da carga em é negativa. A fórmula é:
Perceba que um ponto dentro deste intervalo
Aqui vamos ter os termos referentes à cada uma das cargas, ok? Sendo o termo da esquerda referente à carga da esquerda e o termo da direta a carga da direita. Então substituindo:
Desenvolvendo:
Cancelando os termos da subtração:
Aqui já temos uma resposta bem razoável, mas ainda dá pra simplificar um pouco esse denominador fazendo
Aí o campo fica
Se quiser pode substituir o :
Passo 3
- Para , as duas cargas produzem um campo que aponta na direção positiva de (para direita):
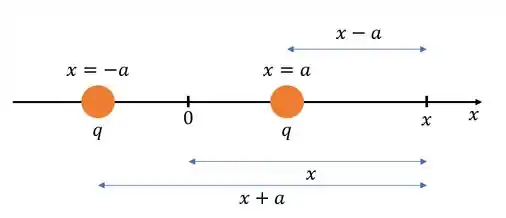
A carga da esquerda está a uma distância do nosso ponto enquanto que a carga da direita está a uma distância , assim
Novamente aqui já temos uma resposta válida, mas é sempre bom simplificar o máximo possível para aquele professor chato né? =P
Lembrando que no denominador podemos escrever ! Expandindo os caras de cima
Substituindo o , finalmente temos
Passo 4
- Para , os campos produzidos pelas duas cargas apontarão para esquerda, ou seja, cada um deles será negativo.
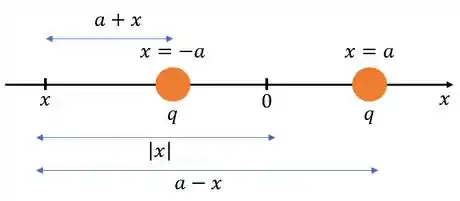
Como , a distância do nosso ponto até a carga da esquerda é (lembrando que ) e da carga da direita é , assim
Essa conta no parênteses grande é igualzinha à conta do passo anterior, então vamos ter como resultado
E fim de papo.
Resposta
Para
Para :
Para