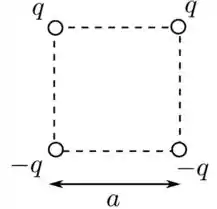
Quatro partículas carregadas são fixadas sobre os vértices de um quadrado de lado , como mostrado na figura abaixo. Suas cargas estão indicadas. Qual é o campo eletrostático produzido pelas quatro partículas no centro do quadrado?
Passo 1
Bom, vamos começar a estudar este exercício considerando a figura abaixo, em que identificamos as cargas de mesmo sinal com a mesma cor. Vamos dizer que , para facilitar a nossa discussão, mas o mesmo valerá para o caso em que .
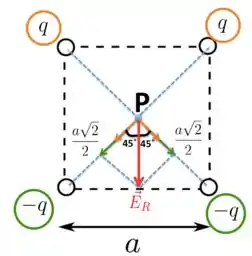
Na figura acima, representamos o centro do quadrado pelo ponto . Este ponto está a uma mesma distância de cada uma das cargas. Como , os campos gerados por essas cargas em laranja sobre o ponto são de afastamento, como indicam os vetores de mesma cor.
Já as outras cargas (portanto negativas), produzem campos de aproximação (vetores em verde), também representados na figura. Os vetores em verde e laranja possuem mesmo módulo, ou seja, eles têm o mesmo tamanho. Na figura, representamos esses vetores com tamanhos diferentes apenas para facilitar a visualização, ok? Mas não se esqueça, como todas as quatro cargas têm o mesmo módulo e estão nos vértices à mesma distância de , o tamanho dos vetores é o mesmo!!
Fica claro da figura que, ao somarmos os vetores, no ponto teremos um campo resultante . Portanto, no centro do quadrado, existe um campo elétrico diferente de zero e nosso próximo passa será calcular explicitamente o seu módulo.
Passo 2
Como todos os módulos dos quatro campos elétricos são iguais no ponto , basta calcularmos o módulo de um deles, projetar na direção e multiplicar o resultado por 4, Blz??
Por isso, o módulo do campo resultante no ponto é dado por
Como , temos que o valor do campo resultante no ponto é:
A direção e sentido do vetor está indicado na Figura.