23) Calcule
h) e é a parte do plano , limitada pelo cilindro , com tal que .
Passo 1
Vamos começar este problema vendo o que vamos fazer para chegar a solução do problema, ok? Inclusive isso é sempre sugerido: sempre coloque em primeiro o lugar o que você terá que fazer para chegar no resultado do problema. Fica a dica 😉!
No caso da integral de superfície, existem três coisinhas básicas:
1º - Parametrizar a superfície .
2º - Encontrar o termo
3º - Trocar os termos da função pelos termos da parametrização.
Assim que você parametrizar, encontrar e trocar é só meter bronca na integral. Bora? 😊
Passo 2
A primeira coisa como vimos é parametrizar a superfície do problema. Mas antes: quem é a superfície dada? Ora, se a gente desenhar conforme o enunciado nos pede chegamos na superfície...
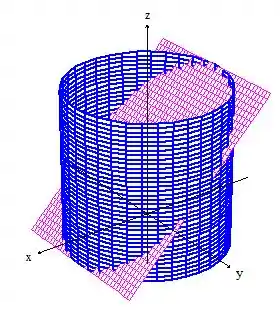
E é ela quem queremos parametrizar!
Pow, veja que estamos trabalhando com um pedaço de plano (a superfície é o plano):
Podemos parametrizar esse plano como uma parametrização explícita, ou seja...
Passo 3
Agora, a gente nunca deve terminar uma parametrização sem ao menos dizer onde estão variando os nossos parâmetros que no caso são E .
Veja que podemos encontrar esses caras, ou melhor, ter uma ideia de onde eles variam fazendo a projeção da superfície no plano :
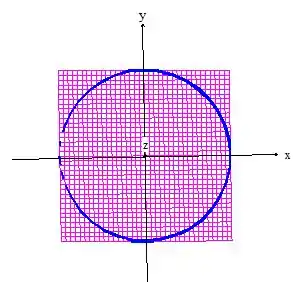
Repare que no caso o e o está sendo delimitado por essa circunferência de equação sendo a mesma do cilindro que a gente te vendo...
Passo 4
Ok, agora de acordo com o nosso roteiro láaaa do passo , o que devemos fazer agora é encontrar o termo e que pode ser encontrado, fazendo:
Onde é o vetor normal da superfície que a gente encontra assim oh (tendo a parametrização em mãos já heim 😉)
No caso, como a parametrização é feita utilizando as parametrizações explicitas podemos evitar esse cálculo chato e seguir o macete aqui oh:
Calculando essas derivadas parciais...
Como o problema nos pediu que , é esse vetor aí mesmo que a gente quer, pois a coordenada dele é positiva 😉!
Então o termo fica sendo...
Passo 5
Ótimo, agora vamos simplesmente trocar os termos da função , pelos termos da parametrização, dessa forma aqui oh:
Como só o que muda...
Passo 6
Prontinho 😊! Agora basicamente temos que voltar para a integral de superfície:
E trocar todos os três caras que descobrimos, onde é substituído pela variação dos parâmetros, desse jeito aqui oh:
Bora calcular a integral?
Passo 7
Como a região é circular de raio ...
Podemos mudar para as coordenadas polares...
Não se esquecendo do Jacobiano
E lembrando que como é um círculo cheio o só pode está dando uma volta completa:
Enquanto o ...
Logo...
Calculando isso