Questão 2: Calcule
Onde e é a parte do paraboloide limitado pelo cilindro e orientado por tal que .
Passo 1
OK! A primeira coisa a fazermos em problemas de cálculo de integrais de superfície do caso vetorial é justamente montarmos um esquema de como vamos chegar à solução. O método que podemos adotar é esse daqui:
- Primeiro parametrizar a superfície.
- Segundo, deveremos encontrar o termo .
- Depois a gente tem que trocar os termos do campo pelos termos da parametrização.
- Por último é só voltar para a integral, substituir e terminar os cálculos.
Vamos nessa então?
Passo 2
Como vimos, o que precisamos fazer nesse primeiro momento, é parametrizar a superfície . Mas por falar nisso... Quem é ela?
Pelo enunciado, estamos trabalhando com um paraboloide ao redor do eixo e passando por ...
Um paraboloide é infinito, por isso, o nosso problema nos limita pelo cilindro de raio ()...
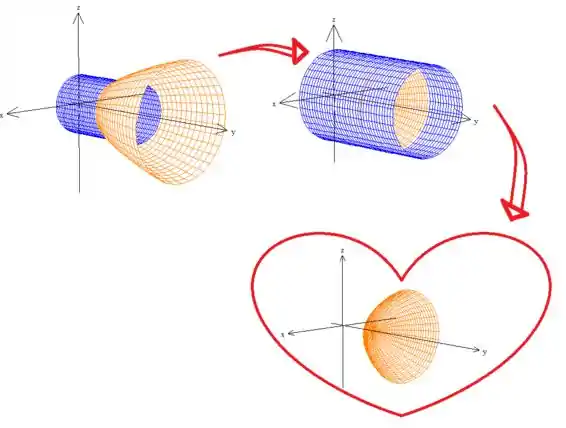
Ou seja, o nosso paraboloide tem um indo de até , pois o encontro do cilindro com o paraboloide é justamente nesse valor:
MAS ATENÇÃO! Embora o enunciado menciona um cilindro, a nossa superfície mesmo é o paraboloide! O cilindro é apenas para delimitar a superfície, até porque ninguém quer um paraboloide indo para o infinito, neh?
Passo 3
OK! Conhecemos a superfície , agora... Qual parametrização podemos utilizar para descrevê-la? Ora, a nossa superfície (o paraboloide) tem uma equação bem explícita:
Então é legal utilizarmos uma parametrização também explícita com os dois parâmetros que precisamos sendo o e ...
Passo 4
Como em qualquer outra parametrização, devemos determinar onde os parâmetros variam. No nosso caso, eles estão variando dentro do cilindro:
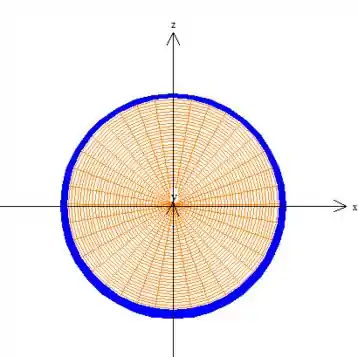
Inclusive, dava para desconfiar, se olharmos para a projeção da superfície no plano , neh? No momento, vamos apenas indicar que o nosso e estão variando dentro desse disco de raio aí:
Depois se precisarmos, a gente o descreve em coordenadas polares. Só não vamos fazer isso agora para não perdermos o foco na solução da integral de superfície ;)
Passo 5
Por falar em integral de superfície... O nosso próximo passo é dedicado para encontrar o termo
O vetor normal , por sua vez...
Calculando essas derivadas parciais...
Como o cálculo de um produto vetorial é um determinante onde...
Ou...
Mas lembre-se que queremos o vetor normal que satisfaz ...
Logo, o vetor normal que buscamos é o inverso desse...
Então...
Passo 6
Como terceira tarefa, precisamos trocar os termos do campo pelos termos da parametrização...
Como na nossa parametrização o único que muda é o (o e o continuam sendo eles mesmos), o nosso campo não muda:
Passo 7
Retornando para a integral então:
Calculando esse produto escalar:
Veja então que trocamos uma integral de superfície por um a integral dupla na região de variação dos parâmetros, como já era esperada mesmo ! Para facilitar a integração, bora trocar as variáveis pelas coordenadas polares:
O Jacobiano dessa mudança é:
Outra equação que nos ajuda muito nessa mudança é equação do círculo:
Passo 8
Toda mudança, nos exige que determinemos onde as variáveis “variam”! No caso, para ver onde o raio e o estão variando, bastam dar uma checada na variação de e :
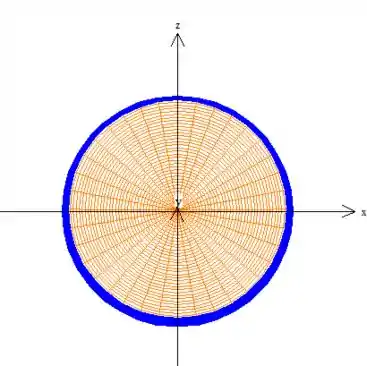
Veja que varia de até o raio máximo da região que é justamente o raio do cilindro (borda azul dessa região )...
Enquanto o dá uma volta de ...
Passo 9
Voltando então para a integral dupla não se esquecendo de multiplicar a função pelo Jacobiano...
Integrando então...
Então...