Integrais de superfície – caso vetorial
Calcule onde e é a parte do hiperboloide limitado pela esfera com a normal que aponta no sentido que se afasta do eixo .
Passo 1
Antes de tudo, vamos pensar que superfície é essa do problema. Temos um hiperboloide cortado por uma esfera:
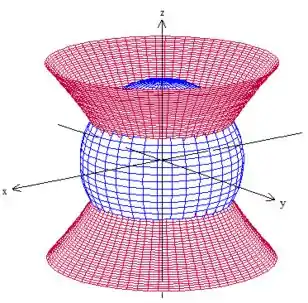
A superfície do problema é a parte do hiperboloide que está dentro da esfera, portanto, isso aqui:
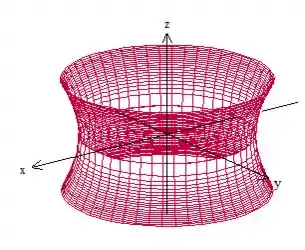
Onde a normal aponta para fora.
Passo 2
Como temos simetria em relação ao eixo e termos quadráticos, vamos parametrizar essa superfíce em coordenadas cilíndricas, ok? Temos:
O que nos dá
Temos duas parametrizações muito parecidas, uma para a parte do hiperboloide que fica acima do plano e outra para a parte que fica abaixo.
OBS: Essas duas superfícies são simétricas em . Se você reparar, a função que vamos integrar também é simétrica em , o que quer dizer que a integral sobre vai ser igual à sobre . Por isso, vamos trabalhar aqui só com e dobrar o resultado, ok?
Como temos a volta completa em torno do eixo , . Para descobrir o intervalo de precisamos descobrir onde o hiperboloide corta a esfera:
Somando as duas equações, temos:
Sabemos então que as superfícies se cortam em , certo?
Como o raio mínimo é , quando , nós sabemos que .
Passo 3
Agora temos que calcular a normal
Temos:
Bom, como o problema diz que a normal aponta para longe de , isso quer dizer, para , a componente da normal ser negativa. Volta lá no desenho se você ficou confuso. Logo, o vetor que queremos é o oposto a esse:
Passo 4
Agora, para calcular essa integral, vamos usar a seguinte fórmula:
Como nós vimos que a integral em vai ser igual à em , temos:
Aplicando os valores que nós temos:
Onde
Escrevendo nas variáveis da parametrização:
Trazendo os intervalos de e :
Passo 5
Agora vamos resolver isso aí. Fazendo: