Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial

Ver Teoria
Exercício 7012345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686971727374757677787980818283

Enunciado

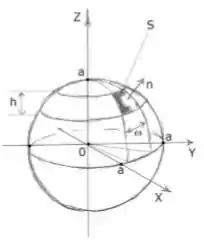
Calcule a integral de superfície ∬ S F → ∙ d S → , onde F → x ,   y ,   z = 1 x , 1 y , 1 z e S é a parte da esfera x 2 + y 2 + z 2 = a 2 , cujo contorno está definido como intercessão da esfera com dois planos horizontais paralelos e dois planos verticais concorrentes, que passam pelo eixo z , conforme à figura abaixo. A distância entre os planos horizontais é h , o ângulo entre os planos verticais é ω , S pertence ao primeiro octante, e o vetor normal aponta fora da esfera.

Passo 1

Vamos começar procurando uma parametrização para a superfície S do problema. Bem... se estamos trabalhando com uma superfície em cima de uma esfera, nada mais natural que pensar em uma parametrização esférica, não acha? Ou seja, vamos fazer

x = a sin ⁡ ϕ cos ⁡ θ

y = a sin ⁡ ϕ sin ⁡ θ

z = a cos ⁡ ϕ

Onde a é o raio da esfera, uma constante portanto!:D Logo, uma parametrização para a superfície S em função de ϕ e θ será

σ ϕ ,   θ = a sin ⁡ ϕ cos ⁡ θ , a sin ⁡ ϕ sin ⁡ θ ,   a cos ⁡ ϕ  

Passo 2

Se a gente se recordar das coordenadas esféricas, θ é um ângulo de variação no plano X Y . Como podemos perceber com o desenho da esfera, esse ângulo θ , varia de ω radianos. Oi? Como assim?

Bem, isso significa que o θ máximo menos o θ mínimo é justamente ω

θ m á x - θ m í n = ω

Portanto, o parâmetro θ inicia no θ m í n e termina no máximo

θ m í n ≤ θ ≤ θ m á x       ⇒         θ m í n ≤ θ ≤ θ m í n + ω

Ok! Mas e o limite desse outro parâmetro aí?! ϕ ...?

Passo 3

Bem, quanto ao ângulo ϕ , aquele ângulo que varia de cima pra baixo no eixo z , ele entra na superfície no plano horizontal de cima, e sai no plano horizontal de baixo. Beleza, e o que significa isso?

Bem, se você notar que um plano horizontal tem a coordenada z constante, ele também terá um ângulo ϕ de entrada e saída também constante. Ora! Sim! Pois ϕ   depende apenas de z , percebeu?

Logo,

ϕ m í n ≤ ϕ ≤ ϕ m á x

ϕ m í n é o ângulo de entrada que só depende do plano horizontal de cima. Como o plano horizontal de cima tem um z constante, z 0 ...

z 0 = a cos ⁡ ϕ m í n

Quanto ao plano de baixo, temos que ele delimita o ângulo máximo e ele está abaixo de z 0 por h unidades. Veja só

z 0 - h = a cos ⁡ ϕ m á x

Passo 4

Beleza, agora nos falta encontrar, aquele termo d S → .

Se a gente se recordar lá da teoria de integrais de superfície no caso vetorial vamos lembrar que

d S → = N →   d ϕ d θ

Onde N → é o vetor normal da superfície, obtida utilizando o produto vetorial das derivadas parciais da superfície. Ou seja,

N → = ∂ σ ∂ ϕ × ∂ σ ∂ θ

Começando a calcular isso pelas derivadas de σ ϕ ,   θ = a sin ⁡ ϕ cos ⁡ θ , a sin ⁡ ϕ sin ⁡ θ ,   a cos ⁡ ϕ   :

∂ σ ∂ ϕ = a cos ⁡ ϕ cos ⁡ θ ,   a cos ⁡ ϕ sin ⁡ θ ,   - a sin ⁡ ϕ

∂ σ ∂ θ = - a sin ⁡ ϕ sin ⁡ θ ,   a sin ⁡ ϕ cos ⁡ θ ,   0

Agora lançando mão do produto vetorial dessas coisas, lembrando que produto vetorial é um determinante onde a primeira linha são os vetores unitários i ^ , j ^ e k ^

∂ σ ∂ ϕ × ∂ σ ∂ θ = i ^ j ^ k ^ a cos ⁡ ϕ cos ⁡ θ a cos ⁡ ϕ sin ⁡ θ - a sin ⁡ ϕ - a sin ⁡ ϕ sin ⁡ θ a sin ⁡ ϕ cos ⁡ θ 0 =

Efetuando o determinante, e juntando os termos ficamos com:

∂ σ ∂ ϕ × ∂ σ ∂ θ = a 2 sin 2 ⁡ ϕ cos ⁡ θ i ^ + a 2 sin 2 ⁡ ϕ sin ⁡ θ j ^ + a 2 sin ⁡ ϕ cos ⁡ ϕ k ^

Ou ainda, em notação vetorial para facilitar a nossa visualização

d S → = ��� σ ∂ ϕ × ∂ σ ∂ θ d ϕ d θ = a 2 sin 2 ⁡ ϕ cos ⁡ θ ,   a 2 sin 2 ⁡ ϕ sin ⁡ θ ,   a 2 sin ⁡ ϕ cos ⁡ ϕ d ϕ d θ

Passo 5

Não podemos esquecer de aplicar essa transformação na função vetorial F → , hein!

F → = 1 x , 1 y , 1 z

F → = 1 a sin ⁡ ϕ cos ⁡ θ , 1 a sin ⁡ ϕ sin ⁡ θ , 1 a cos ⁡ ϕ

Mas note que na integral de superfície, ∬ S F → ∙ d S → ,não estamos interessados em F → sozinho e sim o produto interno dele por d S → , ou seja

F → ∙ d S → =

1 a sin ⁡ ϕ cos ⁡ θ , 1 a sin ⁡ ϕ sin ⁡ θ , 1 a cos ⁡ ϕ ∙ a 2 sin 2 ⁡ ϕ cos ⁡ θ ,   a 2 sin 2 ⁡ ϕ sin ⁡ θ ,   a 2 sin ⁡ ϕ cos ⁡ ϕ d ϕ d θ

Efetuando esse cara aí

= a 2 sin 2 ⁡ ϕ cos ⁡ θ a sin ⁡ ϕ cos ⁡ θ + a 2 sin 2 ⁡ ϕ sin ⁡ θ a sin ⁡ ϕ sin ⁡ θ + a 2 sin ⁡ ϕ cos ⁡ ϕ a cos ⁡ ϕ d ϕ d θ ⇒

E simplificando essas frações, obteremos

F → ∙ d S → = 3 a sin ⁡ ϕ d ϕ d θ

Passo 6

Prontinho! Agora é só jogar toda essa receita na integral. :D Vem comigo!

∬ S F → ∙ d S → = ∫ θ m í n θ m á x ∫ ϕ m í n ϕ m á x 3 a sin ⁡ ϕ d ϕ d θ

∬ S F → ∙ d S → = ∫ θ m í n θ m á x 3 a   - cos ⁡ ϕ ϕ m í n ϕ m á x   d θ

Substituindo os limites em ϕ

∬ S F → ∙ d S → = ∫ θ m í n θ m á x 3 a ( cos ⁡ ϕ m í n - cos ⁡ ϕ m á x ) d θ

Agora integrando em θ , vamos obter

�� S F → ∙ d S → = 3 a ( cos ⁡ ϕ m í n - cos ⁡ ϕ m á x ) ∙ θ θ m í n θ m á x   d θ

∬ S F → ∙ d S → = 3 a ( cos ⁡ ϕ m í n - cos ⁡ ϕ m á x ) θ m á x - θ m í n

Pow! Olha que expressão bacana obtivemos como resultado dessa integral :D

  1. Pra começar, já vimos que θ m á x - θ m í n = ω
  2. Quanto a ( cos ⁡ ϕ m í n - cos ⁡ ϕ m á x ) , se trabalharmos um pouco com aquelas duas expressões que obtivemos com a variação de ϕ :

z 0 = a cos ⁡ ϕ m í n

              z 0 - h = a cos ⁡ ϕ m á x

Ganharemos ( cos ⁡ ϕ m í n - cos ⁡ ϕ m á x ) = h a

Substituindo tudo na integral

∬ S F → ∙ d S → = 3 a h a ω = 3 h ω

Resposta

∬ S F → ∙ d S → = 3 h ω

Exercícios de Livros Relacionados

Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
A temperatura de um ponto da bola com condutividade K é inversamente proporcional à distância do centro da bola. Determine a taxa de transmissão de calor através de uma esfera S de raio a e centro da
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por y = h ( x , z ) e n → é o vetor normal unitário que aponta para a esquerda.
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por x = h ( y , z ) e n → é o vetor normal unitário que aponta para frente (ou seja, para o observador, qua