Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial

Ver Teoria
Exercício 6112345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596062636465666768697071727374757677787980818283

Enunciado

UTFPR. Calculo Avançado. Lista 2 de Exercícios - Cálculo Vetorial. AV1. Questão 3.

3. Determine o fluxo de F ( x , y , z ) = s e n x y z i + x 2 y j + z 2 e x / 5 k através da parte do cilindro 4 y 2 + z 2 = 4 que está acima do plano x y e entre os planos x = - 2 e x = 2 com orientação para cima.

Passo 1

Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nessa questão, temos um caso vetorial de integrais de superfície.

Lembrando um pouquinho da teoria, vemos que esses casos são resolvidos calculando a seguinte integral

∫ ∫ S F · N d A

Onde F é o fluxo parametrizado dado por F ( x , y , z ) = s e n x y z i + x 2 y j + z 2 e x / 5 k e N é um vetor normal paramétrico de S .

Ta lembrado desse método?

Portanto a primeira coisa que fazer é parametrizar a superfície S , calcular o vetor normal a S , aplicar a parametrização em F , obter os limites de integração e calcular a integral!

Parece tranquilo?

Vamos ver como é a região S ?

É dada pela parte de cima desse cilindro elíptico limitado entre x = - 2 e x = 2 .

Bora começar? 😁

Passo 2

Nossa região S é dada por um cilindro elíptico, então vamos parametrizar S .

Lembrando de coordenadas elípticas, tínhamos

x = a r c o s θ y = b r s e n θ

Para uma elipse dada por

x 2 a 2 + y 2 b 2 = 1

Porem, nossa elipse é dada por

4 y 2 + z 2 = 4

Escrevendo por uma forma mais fácil de visualizar a e b

y 2 1 2 + z 2 2 2 = 1

Antes, tínhamos x e y , agora temos y e z .

Fazendo uma analogia entre S e a parametrização em coordenada elípticas, podemos escrever como

y = r c o s θ z = 2 r s e n θ

Mas o que é r ?

Substituindo na equação S , temos

r c o s θ 2 1 2 + 2 r s e n θ 2 2 2 = 1

r 2 cos 2 ⁡ θ + r 2 s e n 2 θ = 1

Colocando r 2 em evidencia e lembrando que s e n 2 θ + c o s 2 θ = 1

r 2 cos 2 ⁡ θ + s e n 2 θ = 1

r 2 = 1

Portanto, temos que

r = 1

Ou seja, nossa parametrização é finalmente

y = c o s θ z = 2 s e n θ

Ou também, como x continua sendo x

P x , θ = x , cos ⁡ θ , 2 s e n θ

Tranquilo até aqui? 👀

Passo 3

Agora vamos em busca do vetor normal a S , pra isso, derivamos P com relação a x e depois com relação a θ e calculamos o produto vetorial entre eles.

Primeiro com relação a x

∂ P ∂ x = ∂ x , cos ⁡ θ , 2 s e n θ ∂ x

Como só temos x no primeiro membro, o resultado é obtido pelo método de derivação polinomial

∂ P ∂ x = x 1 - 1 , 0,0

∂ P ∂ x = 1,0 , 0

Agora derivando com relação a θ , temos

∂ P ∂ θ = ∂ x , cos ⁡ θ , 2 s e n θ ∂ θ

Lembrando do teorema fundamental do cálculo temos que

∂ P ∂ θ = 0 , - s e n θ , 2 cos ⁡ θ

Calculando o produto vetorial entre eles, temos o vetor normal a S

Como no enunciado diz que a orientação é para cima, fazemos ∂ P ∂ θ X ∂ P ∂ x

N = i j k 0 - s e n θ 2 cos ⁡ θ 1 0 0

Calculando esse determinante, temos

N = 0 i + 2 cos ⁡ θ j + s e n θ k

Agora precisamos aplicar a parametrização que fizemos na função vetorial F

F P x , θ = s e n x cos ⁡ θ 2 s e n θ i + x 2 cos ⁡ θ j + 2 s e n θ 2 e x / 5 k

Organizando um pouquinho, temos

F P x , θ = s e n 2 x cos ⁡ θ s e n θ i + x 2 cos ⁡ θ j + 4 s e n 2 θ e x / 5 k

Interessante, não é? 😎

Passo 4

Agora vamos calcular o produto interno de F P x , θ com N

F P x , θ · N = s e n 2 x cos ⁡ θ s e n θ , x 2 cos ⁡ θ , 4 s e n 2 θ e x 5 · 0,2 cos ⁡ θ , s e n θ

F P x , θ · N = 2 x 2 cos 2 ⁡ θ + 4 e x 5 s e n 3 θ

Antes de montar nossa integra, vamos obter nossos limites de integração

Olhando para a imagem da nossa superfície S e fazendo as analogias necessárias onde em coordenadas elípticas tínhamos

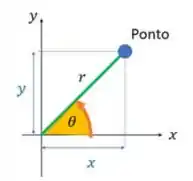
Agora nosso y tomou o lugar do x e nosso z tomou o lugar de y .

Com isso, podemos dizer que o semieixo positivo de y define θ inicial, ou 0 .

Como estamos interessados em z ≥ 0 , podemos dizer que θ varia entre 0 e π

Concorda?

Já x foi dado no enunciado que queremos os valores entre - 2 e 2 .

Portanto, nossos limites de integração serão

0 ≤ θ ≤ π - 2 ≤ x ≤ 2

Logo, conseguimos escrever nossa integral como

∫ 0 π ∫ - 2 2 2 x 2 cos 2 ⁡ θ + 4 e x 5 s e n 3 θ d x d θ

Estamos na reta final! 🤩

Passo 5

Integrando com relação a x pelo método de integração polinomial em x 2 e pelo método de substituição u d u em e x 5 .

Integrando as somas separadamente

∫ 2 x 2 cos 2 ⁡ θ d x = 2 x 2 + 1 2 + 1 cos 2 ⁡ θ = 2 x 3 3 cos 2 ⁡ θ

∫ 4 e x 5 s e n 3 θ d x = 4 s e n 3 θ ∫ e x 5 d x

Fazendo u = x 5 e 5 d u = d x , temos

4 s e n 3 θ ∫ 5 e u d u

Como a integral de e u é igual a e u

4 s e n 3 θ ∫ 5 e u d u = 20 s e n 3 θ e u

Voltando u para x / 5

∫ 4 e x 5 s e n 3 θ d x = 20 s e n 3 θ e x 5

Juntando os resultados novamente, temos

∫ 2 x 2 cos 2 ⁡ θ + 4 e x 5 s e n 3 θ d x = 2 x 3 3 cos 2 ⁡ θ + 20 s e n 3 θ e x 5

Aplicando os limites de integração

∫ - 2 2 2 x 2 cos 2 ⁡ θ + 4 e x 5 s e n 3 θ d x = 2 2 3 3 cos 2 ⁡ θ + 20 s e n 3 θ e 2 5 - 2 - 2 3 3 cos 2 ⁡ θ + 20 s e n 3 θ e - 2 5

Simplificando o resultado

∫ - 2 2 2 x 2 cos 2 ⁡ θ + 4 e x 5 s e n 3 θ d x = 32 3 cos 2 ⁡ θ + 20 e 2 5 - 20 e - 2 5 s e n 3 θ

O que está achando? 👀

Passo 6

Agora integramos o resultado com relação a θ

*   ∫ 32 3 cos 2 ⁡ θ + 20 e 2 5 - 20 e - 2 5 s e n 3 θ d θ

Novamente vamos separar a integral da soma

32 3 ∫ cos 2 ⁡ θ d θ + 20 e 2 5 - 20 e - 2 5 ∫ s e n 3 θ d θ

Para c o s 2 θ podemos escreve-la como uma identidade dada por

c o s 2 θ = 1 2 + c o s 2 θ 2

Logo, reescrevemos a integral como

32 3 ∫ 1 2 + c o s 2 θ 2 d θ

* *   32 3 ∫ 1 2 d θ + ∫ c o s 2 θ 2 d θ

A integral de 1 2 podemos obter pelo método de integração polinomial, já a integral de c o s 2 θ 2 aplicamos o método de substituição u d u

∫ 1 2 d θ = 1 2 θ

∫ s e n 2 θ 2 d θ

Se fizermos u = 2 θ vamos ter d θ = d u 2 , logo

∫ c o s u 4 d u = s e n u 4

Voltando u para 2 θ

∫ c o s 2 θ 4 d θ = s e n 2 θ 4

Substituindo esses resultados em * *

32 3 ∫ θ 2 d θ + ∫ s e n 2 θ 4 d θ = 32 3 1 2 θ + s e n 2 θ 4

Trabalhosa essa questão, não é? 👀

Passo 7

Agora vamos calcular a integral de s e n 3 θ

Antes, vamos reescrever s e n 3 θ como

s e n 3 θ = s e n θ s e n 2 θ

Mas o que é s e n 2 θ ? 1 - c o s 2 θ , correto?

s e n 3 θ = s e n θ 1 - c o s 2 θ

Assim nossa integral será

20 e 2 5 - 20 e - 2 5 ∫ s e n θ 1 - c o s 2 θ d θ

Aplicando o método de substituição u d u sendo u = cos ⁡ θ e d u = - s e n θ d θ

20 e 2 5 - 20 e - 2 5 ∫ - 1 - u 2 d u

Pelo método de integração polinomial, vamos obter

20 e 2 5 - 20 e - 2 5 ∫ - 1 - u 2 d u = - 20 e 2 5 - 20 e - 2 5 u - u 2 + 1 2 + 1

20 e 2 5 - 20 e - 2 5 ∫ 1 - u 2 d u = - 20 e 2 5 - 20 e - 2 5 u - u 3 3

Voltando u para cos ⁡ θ

20 e 2 5 - 20 e - 2 5 ∫ s e n 3 θ d θ = - 20 e 2 5 - 20 e - 2 5 cos ⁡ θ - cos 3 ⁡ θ 3

Com isso, juntando esses resultados em *

∫ 32 3 cos 2 ⁡ θ + 20 e 2 5 - 20 e - 2 5 s e n 3 θ d θ = 32 3 1 2 θ + s e n 2 θ 4 - 20 e 2 5 - 20 e - 2 5 cos ⁡ θ - cos 3 ⁡ θ 3

Estamos quase lá!! 🤩🤩

Passo 8

Aplicando os limites de integração π e 0 .

Para π , temos

θ = π :   32 3 1 2 π + s e n 2 π 4 - 20 e 2 5 - 20 e - 2 5 cos ⁡ π - cos 3 ⁡ π 3

θ = π :   16 π 3 + 0 12 - 20 e 2 5 - 20 e - 2 5 - 1 - - 1 3

θ = π :   16 π 3 + 2 3 20 e 2 5 - 20 e - 2 5

Para 0 , temos

θ = 0 :   32 3 1 2 0 + s e n 2 0 4 - 20 e 2 5 - 20 e - 2 5 cos ⁡ 0 - cos 3 ⁡ 0 3

θ = 0 :   32 3 0 - 0 8 - 20 e 2 5 - 20 e - 2 5 1 - 1 3

θ = 0 : - 2 3 20 e 2 5 - 20 e - 2 5

Subtraindo o resultado de π com o resultado de 0 , temos

16 π 3 + 2 3 20 e 2 5 - 20 e - 2 5 - - 2 3 20 e 2 5 - 20 e - 2 5

16 π 3 + 2 3 20 e 2 5 - 20 e - 2 5 + 2 3 20 e 2 5 - 20 e - 2 5

16 π 3 + 4 3 20 e 2 5 - 20 e - 2 5

Logo o resultado final é

∫ 0 π ∫ - 2 2 2 x 2 cos 2 ⁡ θ + 4 e x 5 s e n 3 θ d x d θ = 16 π 3 + 4 3 20 e 2 5 - 20 e - 2 5

Chegamos à conclusão de que o fluxo de F através de S é de 16 π 3 + 4 3 20 e 2 5 - 20 e - 2 5 .

E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta

∫ 0 π ∫ - 2 2 2 x 2 cos 2 ⁡ θ + 4 e x 5 s e n 3 θ d x d θ = 16 π 3 + 4 3 20 e 2 5 - 20 e - 2 5

Exercícios de Livros Relacionados

Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
A temperatura de um ponto da bola com condutividade K é inversamente proporcional à distância do centro da bola. Determine a taxa de transmissão de calor através de uma esfera S de raio a e centro da
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por y = h ( x , z ) e n → é o vetor normal unitário que aponta para a esquerda.
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por x = h ( y , z ) e n → é o vetor normal unitário que aponta para frente (ou seja, para o observador, qua