23) Calcule
e) e é a parte da superfície de revolução obtida girando o segmento de rata que liga a , em torno do eixo , com tendo a componente não negativa.
Passo 1
Sabemos que o fluxo de um campo sobre uma superfície é dado por uma integral de superfície dessa forma aqui:
Mas se você a desenhar a superfície girando o segmento de reta dado...
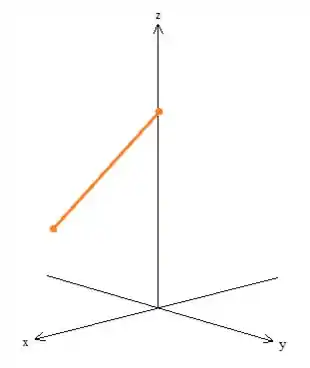
Obtemos o pedacinho do cone...
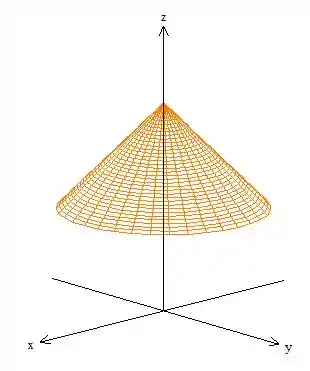
Veja que calcular uma integral de superfície aí vai ser chato, então que tal trocarmos pelo...
Teorema de Gauss
Provavelmente o Teorema de Gauss pode ser a nossa salvação 😉!
Passo 2
Mas não podemos aplicar essa integral assim... De qualquer forma. Precisamos averiguar as condições do Teorema que nos pede:
1º - Uma superfície fechada delimitando o sólido .
2º - Sem singularidades na função Vetorial.
3º - Superfície orientada positivamente.
Vamos passar por cada um deles e verificar se satisfazem ou não 😊!
Passo 3
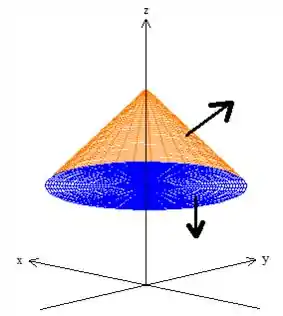
Quanto ao primeiro quesito, ter uma superfície fechada, já falhamos. Afinal de contas a nossa superfície é uma superfície aberta na parte de baixo em :
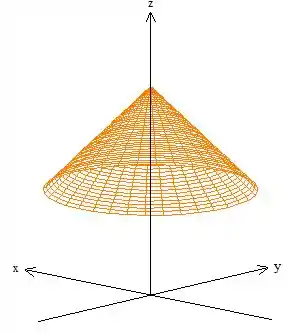
Ora! Temos um fundo faltando um círculo de raio (pois ) em cima do plano , tampemos com esse círculusinho:
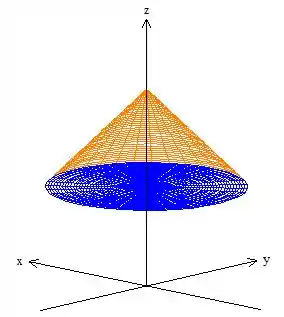
A essa superfície que acabamos de adicionar, daremos um nome de , mas não se preocupe, é apenas um nome ok?
Passo 4
2º - Sem singularidades na função Vetorial:
Esse campo Vetorial funciona em todas as situações, afinal ele não tem nenhuma divisão por ou algo do tipo.
3º - Superfície orientada positivamente:
Bem, isso significa que precisamos de uma superfície com vetores normais saindo do sólido fechado por ela, o que já acontece lá do enunciado afinal o problema nos pediu o vetor normal apontado pra cima. Então é pra fora que o nosso vetor aponta (orientada positivamente 😉)
Passo 5
Bem, com as três condições sendo satisfeitas, podemos aplicar a igualdade do Teorema sem nenhuma restrição...
Aqui só tenho um detalhe que preciso te falar! A integral de superfície do teorema é calculada em cima da superfície que fecha o sólido . E esse cara é
Logo, temos que desmembrar a integral de superfície em duas...
Vamos só fazer mais simplificações aqui... Passando a integral de pro outro lado...
Passo 6
Eu sei que parece loucura trocar o cálculo de uma integral de superfície por outras duas integrais! Mas pode acreditar talvez é o único jeito mesmo ainda mais nesse caso 😐!
Mas vamos começar aqui então pela integral tripla...
O divergente de pode ser calculado facilmente apenas derivando parcialmente...
Como
Calculando as derivadas parciais:
Logo...
Que maravilha 😊!
Passo 7
Concluímos uma etapa, mas ainda nos falta encontrar qual é o resultado da integral de superfície de em cima de superfície que adicionamos, ou seja, a tampa onde ...
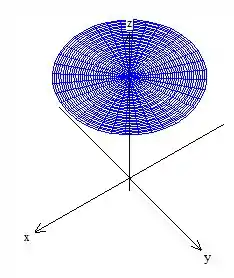
O vetor por ser um vetor normal unitário apontado pra cima... Pode ser escrito como...
Como queremos o vetor contrário, ou seja, o pra baixo...
Resolvendo esse produto escalar...
Agora é só calcular essa integral de superfície do caso escalar 😉!
Passo 8
Precisamos no caso descrever em coordenadas polares...
Calculando o termo ...
Onde...
E .
Vendo que varia de até o raio máximo do cilindro que é e dá uma volta completa...
Passo 9
Calculando a integral...
Passo 10
Veja bem, encontramos o valor da integral em . Mas como vimos do teorema de Gauss...
Então