Questão 4) Dados o campo vetorial e a superfície dada por
Calcule
em que é o vetor unitário apontando para baixo.
Passo 1
Passo 2
Bem, se vamos calcular essa integral de superfície, vamos precisar conhecer bem a Superfície em que estamos trabalhando. Pra isso, basta desenha-la:
Desenhando o plano: ...
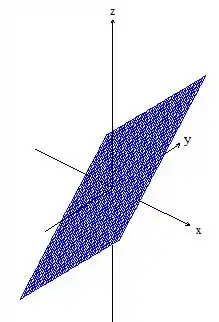
E delimitando pelo cilindro ...
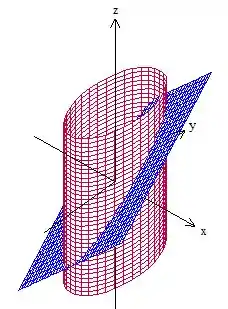
Aqui surge uma dúvida: quem é a superfície aqui? Cara, a superfície sempre será a igualdade (o plano) ok? O cilindro só está ali pra indicar onde o e o variam (delimitando a plano que queremos).
Passo 3
Como a superfície, repito, é o plano e sua equação é bem explícita em função de , podemos parametrizar como uma parametrização explícita:
Então a superfície de uma forma mais legal...
Passo 4
Onde os parâmetros variam mesmo?
O enunciado diz que a região é a interior ao cilindro
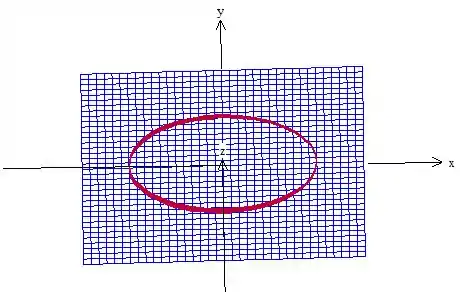
Então por hora, vamos apenas dizer que os parâmetros variam nessa região ai da elipse, ok? Depois se precisar, descrevemos em coordenadas polares.
Passo 5
Vamos achar agora o valor do nosso vetor normal
Calculando cada derivada separadamente
Como o vetor que ele nos pede tem que estar apontado pra baixo, basta que invertemos o sinal desse vetor encontrado (para a coordenada ficar negativa):
Passo 6
Substituindo, por conseguinte, os termos da parametrização...
Na função que queremos a integral dupla, ou seja...
Passo 7
Voltando para a integral de superfície...
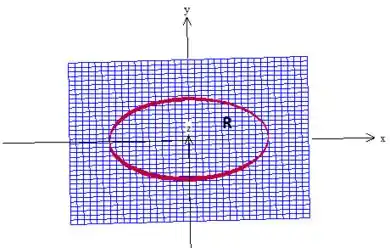
Agora, repare que estamos trabalhando com uma integral dupla em uma região elíptica. Podemos então usar as mudanças para coordenadas elípticas ;)
Onde varia de até (quando a elipse é a maior possível), enquanto que dá uma volta completa:
Substituindo na integral dupla...
E calculando...