Seja a parte do hiperboloide com , limitada por , orientada com tal que .
- Dê uma parametrização de e uma expressão para o campo de vetores normais .
- Calcule , onde .
Passo 1
Letra a)
Antes de tudo, vamos desenhar essa superfície, para entender melhor o que está acontecendo. Temos um hiperboloide de uma folha com simetria no eixo :
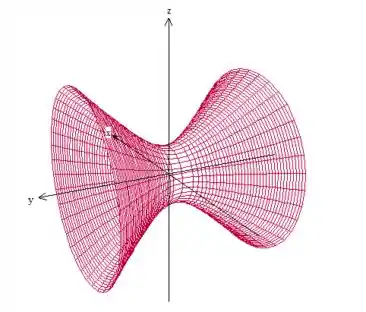
Como o problema fala da parte da superfície do hiperboloide que se encontra acima do círculo de raio , vamos trazer esse círculo para cima, até ele cortar a superfície vermelha:
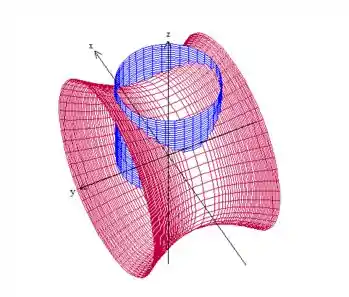
Sacou? A superfície do problema é essa parte do hiperboloide que está dentro do cilindro azul.
Passo 2
Agora vamos parametrizar essa superfíce. Qual será a melhor maneira para parametrizar o paraboloide ? Vamos usar logo e como parâmetros, para ser mais simples:
Como vemos pela figura, o domínio dessa superfície é a circunferência de raio , a projeção da região no plano , logo:
Passo 3
Agora temos que calcular a normal
Temos:
Bom, como o problema diz que a normal aponta para cima , e temos a coordenada positiva nesse vetor, sabemos que é esse mesmo o que queremos.
Passo 4
Temos agora que normalizar aí, pois:
Temos
Logo, o campo que queremos é dado por:
Passo 5
Letra b)
Agora, para calcular essa integral, vamos usar a seguinte fórmula:
Aplicando os valores que nós temos:
Escrevendo o campo em função das variáveis da parametrização, temos:
A integral fica então
Passo 6
Beleza, agora precisamos escrever essa região . Como se trata de uma circunferência , vamos usar coordenadas polares:
Temos e . Aplicando na integral:
Integrando isso aí:
Lembrando da relação:
Temos:
Resposta
- ;