Seja a superfície de revolução obtida girando a curva , definida pela equação
Em torno do eixo com vetor normal apontando para o lado do eixo de revolução. Calcule o fluxo do campo vetorial
Através da superfície de revolução .
Passo 1
O problema nos pede o seguinte:
Então, antes de tudo, vamos descobrir quem é . Podemos parametrizar a curva que gera como:
Lembra daquele macete para parametrizar superfície de revolução?
Sendo uma curva do plano parametrizada por , a parametrização da superfície gerada quando rotacionamos em torno do eixo é:
Em resumo: a variável , paralela ao eixo de rotação não se altera: .
As outras duas variáveis serão escritas em função de , a coordenada da parametrização da curva que nos restou. Como é pertencente ao plano da curva, apresentará e , não pertencente, apresentará .
Como temos uma volta completa:
Foi?
Passo 2
Agora nós precisamos da normal a :
Agora imagine essa curva girando em torno do eixo :
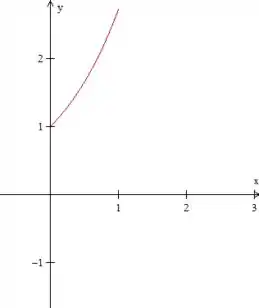
Para a normal apontar para esse eixo, ou seja, para dentro de , a componente da nomal deve ser positiva, percebeu? Isso porque a normal deve estar inclinada para a direita no gráfico.
Então, sabemos que o vetor que queremos é o mesmo que encontramos.
Passo 3
Vamos, então, usar a fórmula:
Isso nos dá