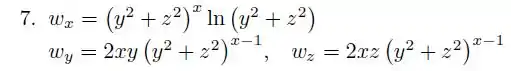![]()
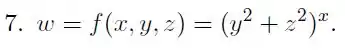
Passo 1
Vamos começar pela derivada parcial em relação a .
Beleza, mas como diabos vamos derivar em relação a se está no expoente?!
Para fazer essa derivada parcial, vamos usar a derivação logarítmica. Assim:
Aplicamos dos dois lados:
Usamos as propriedades do :
Derivamos os dois lados, usando a regra da cadeia e do produto:
Passo 2
Ok, chegamos a expressão quase pronta da derivada. Mas, como estamos derivando em relação a , temos que considerar apenas as derivadas em relação a . Assim:
Sabemos que , então
Passo 3
Agora vamos fazer a derivada parcial em relação a .
Essa é mais fácil, né? Porque agora o que tá no expoente é considerado uma constante. Aí é só fazer a derivada normal como estamos acostumados.
Usando a regra da cadeia:
Passo 4
Por fim, vamos terminar logo isso com a derivada parcial em relação a .
Do mesmo jeito que fizemos no passo 2:
Resposta