7 - A janela de uma casa tem a forma de um retângulo com um triângulo isósceles no topo. Se o perímetro da janela é e esta deve coletar a maior quantidade de energia solar possível, mostre que o ângulo da base do triângulo é radianos.
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nessa questão, vamos resolver um problema de maximização. Foi dito que temos uma janela quadrada com um triângulo de dois lados iguais, sendo que o perímetro total da janela é de . Vamos desenhar seu formato pra facilitar nossa visualização do problema
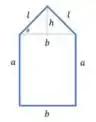
O que estamos buscando é para as medidas da janela que fazem o máximo de luz entrar, ou seja, a área da janela seja máxima, temos que provar que o ângulo é igual a .
Tem alguma ideia de como podemos começar?? 🤔🤔
A princípio, podemos começar montando nossas equações de área e perímetro da janela, que tal?
Bora lá!
Passo 2
Primeiro vamos montar nossa equação que descreve a área da nossa janela. Essa equação é formada pela área do quadrado e pelo triângulo .
Temos que deixar em função de , então temos que substituir
Mas o que é ?
é o seno de multiplicado pela hipotenusa , correto?
Logo
E o que é ?
Podemos dizer que é igual a dividido por , não é? Então podemos dizer também que
Substituindo em , temos
Lembrando de propriedades trigonométricas, o que é ? , lembra? Então
Logo, essa é a função que temos que maximizar! 😎😎
Passo 3
Mas antes, temos que substituir a equação do perímetro, pois ela que delimita o perímetro que temos
Sabemos que , então
Temos que substituir essa equação em , então vamos isolar em um lado da equação e substituir em
Substituindo em
Para obter os parâmetros em que é o maior possível, temos que encontrar o ponto crítico em que determina o ponto máximo de .
Isso é bem familiar, não é? Como vimos, temos que derivar em relação a e e igualar a . Assim vamos obter um sistema e a solução desse sistema será os valores que vamos verificar.
Entendeu?
Passo 4
Primeiro vamos derivar com relação a .
Sabemos que a derivada de uma soma é igual a soma das derivadas, então
Todas essas derivadas são obtidas pelo método de derivação polinomial. Neste método, multiplicamos a variável pela potência e subtraímos do seu expoente.
Substituindo esses resultados em , temos
Igualando a , obtemos a primeira equação do nosso sistema.
Tranquilo até aqui?
Passo 5
Agora vamos derivar com relação a
Como estamos derivando com relação a , a variável se comporta como uma constante, então onde não temos para derivar, a derivada é pelo mesmo princípio da derivada de uma constante.
Podemos tirar as constantes para fora das derivadas e obter os resultados por meio do teorema fundamental do cálculo.
Substituindo esses resultados em , temos
Com isso, encontramos nossas duas equações.
Passo 6
Vamos solucionar o sistema dado por
Começando pela segunda equação, temos
A primeira opção não pode ser, já que não pode ser uma solução para nosso problema, e não existe. Então obrigatoriamente
Escrevendo como e como , temos
Para a igualdade ser satisfeita, apenas nosso numerador pode ser , então
Calculando o , temos
Esse era o ângulo que buscávamos, não é? 😎
É isso! Essa resolução te ajudou? Responde Aí! ✌
